 Problem P. 5199. (February 2020)
Problem P. 5199. (February 2020)
P. 5199. A piece of thin and rigid metal wire of length \(\displaystyle \ell\) has a shape of a circular arc. Each end of the wire is attached to a thin thread of length \(\displaystyle \ell\) and the other ends of the threads are fixed at the centre of the circular arc, \(\displaystyle O\), as shown in the figure. The period of the pendulum, which can swing with small amplitude in the vertical plane of the figure, is \(\displaystyle T_1\). If the metal wire is straightened then the pendulum with the altered shape has a period of \(\displaystyle T_2\), when it swings about \(\displaystyle O\) in the plane of the figure, with small amplitude. What is the ratio \(\displaystyle T_2/ T_1\)?
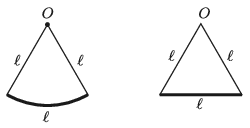
(5 pont)
Deadline expired on March 10, 2020.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mindkét esetben alkalmazhatjuk a fizikai inga lengésidejének
\(\displaystyle T=2\pi\sqrt{\frac{\Theta}{mgs}}\)
képletét, ahol \(\displaystyle s\) a tömegközéppont és az \(\displaystyle O\) pont távolsága, \(\displaystyle \Theta\) pedig az \(\displaystyle O\) pontra vonatkozó tehetetlenségi nyomaték.
Az első esetben a körív nyílásszöge \(\displaystyle 2\alpha=1\) radián (kb. \(\displaystyle 57{,}3^\circ\)), a tehetetlenségi nyomaték pedig \(\displaystyle m\ell^2\), hiszen a körív minden pontja \(\displaystyle \ell\) távolságra van a forgástengelytől. A súlypont és az \(\displaystyle O\) pont távolsága az
\(\displaystyle s=\frac{2(R^3-r^3)}{3(R^2-r^2)}\,\frac{\sin\alpha}{\alpha}\)
összefüggésből (lásd pl. Négyjegyű függvénytáblázatok 197. oldalát) határozható meg, ha az \(\displaystyle R\approx r\approx \ell\) határesetet vizsgáljuk:
\(\displaystyle s=\frac{\sin\alpha}{\alpha}\ell\approx 0{,}96\,\ell.\)
Ezek szerint
\(\displaystyle T_1=2\pi\sqrt{1{,}04\,\frac{\ell}{g}}. \)
A második esetben (a kiegyenesített fémhuzalnál) a tömegközéppont a huzal középpontjánál lesz, tehát
\(\displaystyle s=\ell\,\cos30^\circ\approx 0{,}866\,\ell,\)
a tehetetlenségi nyomaték pedig a Steiner-tétel alapján
\(\displaystyle \Theta=\frac{1}{12}m\ell^2+m\ell^2\,\cos^2 30^\circ=m\ell^2\left(\frac{1}{12}+\frac{3}{4}\right)=\frac{5}{6}m\ell^2.\)
A lengésidő ebben az esetben:
\(\displaystyle T_2=2\pi\sqrt{0{,}96\frac{\ell}{g}}.\)
A keresett arány:
\(\displaystyle \frac{T_2}{T_1}=\sqrt{ \frac{0{,}96}{1{,}04}} \approx 0{,}96.\)
Statistics:
34 students sent a solution. 5 points: Balázs 825 Ádám , Bokor Endre, Fekete Levente, Fonyi Máté Sándor, Györgyfalvai Fanni, Jánosik Áron, Kertész Balázs, Ludányi Levente, Sas 202 Mór, Téglás Panna, Toronyi András, Török 111 László, Vass Bence, Viczián Anna. 4 points: Fekete András Albert, Fülöp Sámuel Sihombing, Hamar Dávid, Horváth 999 Anikó, Nagyváradi Dániel, Schäffer Bálint, Sepsi Csombor Márton, Somlán Gellért, Szabó 314 László, Tóth Ábel. 3 points: 3 students. 2 points: 2 students. 1 point: 2 students. 0 point: 3 students.
Problems in Physics of KöMaL, February 2020
