 |
A P. 5219. feladat (2020. április) |
P. 5219. Sík vidéken egy rét közepén gémeskút áll, függőleges oszlopa fele olyan magas, mint amilyen hosszú a gém. A rét szélére érve \(\displaystyle 2{,}3^\circ\)-os látószögben látjuk a tőlünk 100 méterre, pontosan északra lévő gémeskút oszlopát. A szemünk 165 cm magasan van a talaj fölött. A gém kelet–nyugat irányú, és a közepénél támaszkodik az oszlopra.
Ezt követően 1 m/s állandó sebességgel közelítjük meg a kutat. Számítsuk ki és ábrázoljuk vázlatosan, hogyan változik az idő függvényében a gém látószöge az elindulásunktól a kúthoz érkezésünkig!
Tankönyvi feladat nyomán
(4 pont)
A beküldési határidő 2020. május 11-én LEJÁRT.
Megoldás. Mivel az oszlop látószöge kezdetben elég kicsi, az egyenes, függőleges oszlop magasságát jó közelítéssel helyettesíthetjük a megfelelő (100 m sugarú, \(\displaystyle 2{,}3^\circ\)-os nyílásszögű) körív hosszával. Mivel \(\displaystyle 2{,}3^\circ=0{,}040~\)radián, az oszlop magassága \(\displaystyle \ell=100\cdot0{,}040= 4{,}0\) méter, a gém hossza pedig \(\displaystyle 2\ell=8{,}0\) méter.
Ahogy közeledünk a kúthoz, \(\displaystyle t\) idő elteltével az oszloptól mért távolságunk (SI egységekben) \(\displaystyle 100-t\), A gém közepétől (az oszlop tetejétől) mért távolságunk \(\displaystyle t\) idővel a rétre lépésünk után
\(\displaystyle d(t)=\sqrt{(100-t)^2+(4-1{,}65)^2}.\)
A gém teljes látószögét \(\displaystyle 2\varphi(t)\)-vel jelölve felírhatjuk, hogy
| \(\displaystyle (1)\) | \(\displaystyle \tg\varphi(t)=\frac{ \ell }{d(t)}=\frac{4{,}0}{\sqrt{(100-t)^2+ 5{,}52}}.\) |
Mindaddig, amíg nem érünk a kút közvetlen közelébe (mondjuk a \(\displaystyle 0\le t \le 80~{\rm s}\) időintervallumban) a látószög így számolható:
\(\displaystyle 2\varphi\approx\frac{8}{100-t}~\text{radián}=\frac{4{,}6^\circ}{1-0{,}01\,t},\)
de \(\displaystyle t\approx 10\) s-nál már a pontosabb (1) összefüggést kell alkalmaznunk. A gém legnagyobb látószöge (amikor éppen az oszlopnál vagyunk): \(\displaystyle 2\varphi_\text{max}\approx120^\circ.\)
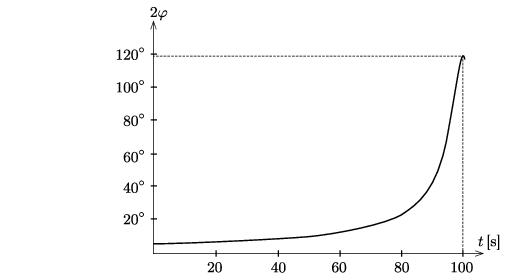
Megjegyzés. Ekkora szöget a mozdulatlan szemünk már nem, vagy csak igen nehezen tud ,,befogni''. Ilyen és ezt meghaladó látószögű tárgyakat csak úgy észlelhetünk, ha a tekintetünk ide-oda cikázik.
Statisztika:
27 dolgozat érkezett. 4 pontot kapott: Beke Zsolt, Bekes Barnabás, Csapó Tamás, Endrész Balázs, Fiam Regina, Jánosik Áron, Kondor Botond Dávid, Kotán Tamás, Ludányi Levente, Páhán Anita Dalma, Schäffer Bálint, Szabó 314 László, Takács Dóra, Téglás Panna. 3 pontot kapott: Györgyfalvai Fanni. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 8 versenyző.
A KöMaL 2020. áprilisi fizika feladatai

