 Problem P. 5219. (April 2020)
Problem P. 5219. (April 2020)
P. 5219. There is a shadoof in the middle of a meadow in a plain. Its vertical pole has half the length of its horizontal beam. Reaching the rim of the meadow, the shadoof is at a distance of 100 m from us towards the north. Observing the shadoof from the rim of the meadow the angle subtended by its vertical pole is \(\displaystyle 2.3^\circ\). Our eyes are at a height of 165 cm, the horizontal beam is east–west and is supported by the pole at its centre.
We walk towards the shadoof at a constant speed of 1 m/s. Calculate and sketch how the angle subtended by the shadoof change over time as we walk from the rim of the meadow to the shadoof until we reach it.
(4 pont)
Deadline expired on May 11, 2020.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel az oszlop látószöge kezdetben elég kicsi, az egyenes, függőleges oszlop magasságát jó közelítéssel helyettesíthetjük a megfelelő (100 m sugarú, \(\displaystyle 2{,}3^\circ\)-os nyílásszögű) körív hosszával. Mivel \(\displaystyle 2{,}3^\circ=0{,}040~\)radián, az oszlop magassága \(\displaystyle \ell=100\cdot0{,}040= 4{,}0\) méter, a gém hossza pedig \(\displaystyle 2\ell=8{,}0\) méter.
Ahogy közeledünk a kúthoz, \(\displaystyle t\) idő elteltével az oszloptól mért távolságunk (SI egységekben) \(\displaystyle 100-t\), A gém közepétől (az oszlop tetejétől) mért távolságunk \(\displaystyle t\) idővel a rétre lépésünk után
\(\displaystyle d(t)=\sqrt{(100-t)^2+(4-1{,}65)^2}.\)
A gém teljes látószögét \(\displaystyle 2\varphi(t)\)-vel jelölve felírhatjuk, hogy
| \(\displaystyle (1)\) | \(\displaystyle \tg\varphi(t)=\frac{ \ell }{d(t)}=\frac{4{,}0}{\sqrt{(100-t)^2+ 5{,}52}}.\) |
Mindaddig, amíg nem érünk a kút közvetlen közelébe (mondjuk a \(\displaystyle 0\le t \le 80~{\rm s}\) időintervallumban) a látószög így számolható:
\(\displaystyle 2\varphi\approx\frac{8}{100-t}~\text{radián}=\frac{4{,}6^\circ}{1-0{,}01\,t},\)
de \(\displaystyle t\approx 10\) s-nál már a pontosabb (1) összefüggést kell alkalmaznunk. A gém legnagyobb látószöge (amikor éppen az oszlopnál vagyunk): \(\displaystyle 2\varphi_\text{max}\approx120^\circ.\)
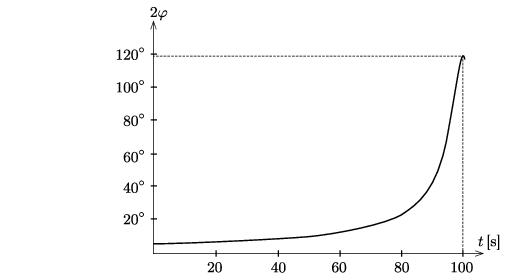
Megjegyzés. Ekkora szöget a mozdulatlan szemünk már nem, vagy csak igen nehezen tud ,,befogni''. Ilyen és ezt meghaladó látószögű tárgyakat csak úgy észlelhetünk, ha a tekintetünk ide-oda cikázik.
Statistics:
27 students sent a solution. 4 points: Beke Zsolt, Bekes Barnabás, Csapó Tamás, Endrész Balázs, Fiam Regina, Jánosik Áron, Kondor Botond Dávid, Kotán Tamás, Ludányi Levente, Páhán Anita Dalma, Schäffer Bálint, Szabó 314 László, Takács Dóra, Téglás Panna. 3 points: Györgyfalvai Fanni. 2 points: 4 students. 1 point: 8 students.
Problems in Physics of KöMaL, April 2020
