Problem P. 5238. (May 2020)

P. 5238. An electric toy car with a mass of \(\displaystyle m_0\), and with a load of mass \(\displaystyle m\) on it, moves upwards at a constant speed along a slope of elevation angle of \(\displaystyle \alpha\). The electric motor, which drives the wheels of radius \(\displaystyle r\), can be modelled, when it operates in a steady rate, with a resistor of resistance \(\displaystyle R\) which is connected in series with a circuit element, whose voltage \(\displaystyle U\) is proportional to the angular velocity of the axle \(\displaystyle \omega\) (\(\displaystyle U=\gamma \omega\)). The current \(\displaystyle I\) that flows through it is proportional to the torque \(\displaystyle M\) exerted by the axles \(\displaystyle (I=M/\gamma)\). The toy car is powered by a battery of e.m.f. \(\displaystyle U_0\) and internal resistance of \(\displaystyle R_{\mathrm{b}}\).

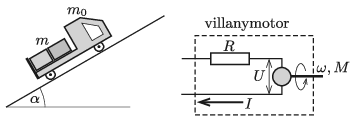
Data: \(\displaystyle m=300\) g, \(\displaystyle \alpha=30^\circ\), \(\displaystyle r=2\) cm, \(\displaystyle \gamma=1.2\) Vs, \(\displaystyle U_0=4{,}5\) V, \(\displaystyle R=0{,}8~\Omega\), \(\displaystyle R_\text{b}=1.2~\Omega\). (The coefficient of static friction between the wheels and the slope is high enough, so the car does not slip.)

\(\displaystyle a)\) At what constant speed does the toy car travel if the mass of the load on it is \(\displaystyle m=600\) g?

\(\displaystyle b)\) At what load of \(\displaystyle m\) will efficiency of the transport of the load be the best? (Efficiency is the ratio of the energy used to lift the load to the energy delivered by the battery.)

(5 pont)

Deadline expired on June 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ha az autó \(\displaystyle v\) sebességgel halad felfelé a lejtőn, akkor a kerekeinek szögsebessége \(\displaystyle \omega=v/r\), a villanymotor modelljében szereplő áramköri elemre (ideális motorra)

\(\displaystyle U=\gamma \frac{v}{r} \)

feszültség jut.

Az áramkörben folyó \(\displaystyle I\) áram hatására az \(\displaystyle R_{\rm b}\) belső ellenálláson és az \(\displaystyle R\) ,,terhelő ellenálláson" összesen \(\displaystyle I(R_{\rm b}+R)\) feszültség esik, így a huroktörvény szerint

\(\displaystyle U_0-I(R_{\rm b}+R)-U=0.\)

Megjegyzés. A motor által leadott mechanikai teljesítmény: \(\displaystyle P=M\omega\) az áramköri elem által felvett \(\displaystyle UI\) elektromos teljesítménnyel egyenlő; emiatt nevezhetjük ezt az áramköri elemet ideális (100%-os hatásfokú) motornak. A motor veszteségét az ideális motorral sorosan kapcsolt \(\displaystyle R\) ellenálláson fejlődő Joule-hővel vesszük figyelembe.

A motor mechanikai munkája az \(\displaystyle \alpha\) hajlásszögű lejtőn \(\displaystyle v\) sebességgel haladó, a teherrel együtt összesen \(\displaystyle m_0+m\) tömegű autó helyzeti energiájának növekedését fedezi:

\(\displaystyle P=\frac{\Delta E_\text{helyzeti}}{\Delta t}=\frac{(m_0+m)g\sin\alpha\,v\Delta t} {\Delta t},\)

vagyis

\(\displaystyle UI=(m_0+m)g\,v\sin\alpha,\)

tehát

\(\displaystyle I=\frac{P}{U}=\frac{r}{\gamma}(m_0+m)g \sin\alpha.\)

(Érdekes, hogy az áramerősség nem függ az autó sebességétől.)

A fenti egyenletekből:

\(\displaystyle U_0-\frac{r}{\gamma}(R_{\rm b}+R)(m_0+m)g\sin\alpha-\frac{v}{r}\gamma=0,\)

ahonnan a játékautó sebessége kifejezhető:

\(\displaystyle v=\frac{r}{\gamma}U_0-\frac{r^2}{\gamma^2} (R_{\rm b}+R)(m_0+m)g\sin\alpha=7{,}25~\frac{\rm cm}{\rm s}.\)

\(\displaystyle b)\) Hatásfok maximalizálása.

A hasznos teljesítmény az előző részben megkapott sebességformula felhasználásával:

\(\displaystyle P_\text{hasznos}=mg\sin\alpha \cdot v=mg\sin\alpha\left(\frac{r}{\gamma}U_0-\frac{r^2}{\gamma^2}(R_{\rm b}+R)(m_0+m)g\sin\alpha\right).\)

Az áramerősség ismeretében a telep által leadott összes teljesítmény:

\(\displaystyle P_\text{telep}=U_0I=\frac{r}{\gamma} U_0(m_0+m)g \sin\alpha.\)

A hatásfok a két teljesítmény hányadosa:

\(\displaystyle \eta(m)=\frac{P_\text{hasznos}}{P_\text{telep}}=\frac{m}{m_0 +m}-\frac{r (R_{\rm b}+R)g \sin\alpha}{U_0\gamma}\cdot m.\)

Ennek a függvénynek keressük a maximumát.

A \(\displaystyle k=\frac{r (R_{\rm b}+R)g \sin\alpha}{U_0\gamma}\) jelölés bevezetésével \(\displaystyle \eta\) így is felírható:

\(\displaystyle \eta=\frac{m}{m+m_0}-km=(1+km_0)-\left(\frac{m_0}{m+m_0}+k(m+m_0)\right),\)

ahonnan a számtani és mértani közepekre vonatkozó egyenlőtlenség szerint

\(\displaystyle \eta\le 1+km_0-2 \sqrt{km_0}=\left(1-\sqrt{km_0}\right)^2.\)

Mivel a megadott számadatok mellett \(\displaystyle k\approx \frac{1}{27\,\rm kg}\), \(\displaystyle \eta\) legnagyobb értéke kb. 80%, és ezt a hatásfokot akkor érheti el a játékautó, ha a terhelése

\(\displaystyle m=\sqrt{\frac{m_0}{k}}-m_0\approx 2{,}55~\rm kg.\)

Statistics:

12 students sent a solution.
5 points:	Békési Ábel, Bonifert Balázs, Fekete András Albert, Kertész Balázs, Selmi Bálint, Somlán Gellért, Toronyi András, Viczián Anna.
4 points:	Bokor Endre, Horváth 999 Anikó.
3 points:	2 students.

Problems in Physics of KöMaL, May 2020