 Problem P. 5273. (December 2020)
Problem P. 5273. (December 2020)
P. 5273. A cuboid of mass \(\displaystyle m = 0.5\) kg, base-side \(\displaystyle a = 20\) cm and of height \(\displaystyle b=10\) cm is initially held at rest on the top of a right-angled inclined plane of mass \(\displaystyle M\) shown in the figure. The angle of elevation of the inclined plane is \(\displaystyle \alpha= 30^\circ\) and its height is \(\displaystyle h= 60\) cm. The cuboid is released at a certain moment. Friction is negligible everywhere.
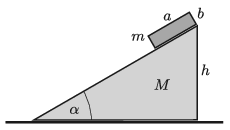
\(\displaystyle a)\) What is the ratio of the speeds of the two objects when the cuboid touches the ground?
\(\displaystyle b)\) How long does it take for the cuboid to reach the ground?
\(\displaystyle c)\) How much distance is covered by the cuboid?
(5 pont)
Deadline expired on January 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Jelöljük a gyorsulásokat és a erőket az ábrán látható módon.
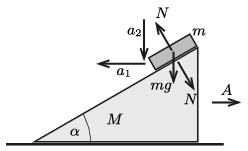
A lejtő mozgásegyenlete:
| \(\displaystyle (1)\) | \(\displaystyle MA=N\,\sin\alpha.\) |
Ha a lecsúszó téglatest vízszintes irányú gyorsulása (a talajhoz képest) \(\displaystyle a_1\), a függőleges gyorsulása pedig \(\displaystyle a_2\), akkor a mozgásegyenletei:
| \(\displaystyle (2)\) | \(\displaystyle N \sin\alpha=ma_1,\) |
illetve
| \(\displaystyle (3)\) | \(\displaystyle mg-N\cos\alpha=ma_2.\) |
A téglatest mindvégig a lejtőn marad, ennek feltétele:
| \(\displaystyle (4)\) | \(\displaystyle a_2=\left(a_1+A\right)\tg\alpha.\) |
Az (1)-(4) egyenletrendszer megoldása:
\(\displaystyle A=\frac{m\sin\alpha\cos\alpha}{m\sin^2\alpha+M}\,g=1{,}89~ \frac{\rm m}{s^2},\)
\(\displaystyle a_1=\frac{M\sin\alpha\cos\alpha}{M+m\sin^2\alpha}\,g=3{,}78~ \frac{\rm m}{ s^2},\)
\(\displaystyle a_2= \frac{(M+m)\sin^2\alpha}{M+m\sin^2\alpha}\,g=3{,}27~ \frac{\rm m}{ s^2},\)
és végül
\(\displaystyle N=\frac{M \cos\alpha}{M+m\sin^2\alpha}\,mg=3{,}78~ \rm N.\)
\(\displaystyle b)\) Függőleges irányban a téglatest \(\displaystyle s=h-a\sin\alpha=0{,}5~\rm m\)-t mozdul el. A mozgás ideje:
\(\displaystyle t=\sqrt{\frac{2s}{a_2}}=0{,}55~\rm s.\)
\(\displaystyle a)\) A lejtő sebessége a kérdéses pillanatban:
\(\displaystyle V^{\rm (max)}=At=1{,}04~\frac{\rm m}{\rm s},\)
míg a lejtőn csúszó téglatest legnagyobb sebességének komponensei:
\(\displaystyle v_{1\rm max}=a_1t=2{,}08~\frac{\rm m}{\rm s},\qquad v_{2\rm max}=a_2t=1{,}81~\frac{\rm m}{\rm s},\)
a sebességének nagysága tehát
\(\displaystyle v=\sqrt{v_{1\rm max}^2+v_{2\rm max}^2}=2{,}76~\frac{\rm m}{\rm s}.\)
\(\displaystyle c)\) A téglatest elmozdulásvektorának komponensei:
\(\displaystyle s_1=\frac{a_1}{2}t^2=0{,}57~{\rm m}; \qquad s_2=\frac{a_2}{2}t^2=0{,}67~{\rm m}=0{,}5~{\rm m},\)
az elmozdulás nagysága (vagyis a megtett útja):
\(\displaystyle \ell=\sqrt{s_1^2+s_2^2}=0{,}76~\rm m.\)
II. megoldás. A feladatot az energia- és a lendületmegmaradás tételének alkalmazásával is meg lehet oldani.
Jelöljük a lejtő gyorsulását \(\displaystyle A\)-val, a téglatestnek a lejtőhöz viszonyított gyorsulását pedig \(\displaystyle a_0\)-lal! A lecsúszás \(\displaystyle t\) ideje alatt a megfelelő sebességek: \(\displaystyle V=At\) és \(\displaystyle v_0=a_0t\).
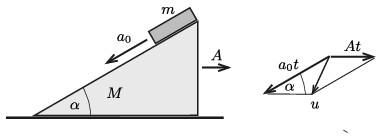
A téglatest sebességének vízszintes komponense a talajhoz képest
\(\displaystyle v_1=a_0t\cos\alpha-At,\)
a sebesség nagysága pedig (ismét a talajhoz viszonyítva) a koszinusz-tételt alkalmazásával:
| \(\displaystyle (5)\) | \(\displaystyle u=\sqrt{v_0^2+V^2-2v_0V\cos\alpha}=t\sqrt{a_0^2+A^2-2a_0A\cos\alpha}.\) |
A lendületmegmaradás tétele szerint
\(\displaystyle MAt=m\left(a_0\cos\alpha-A\right)t,\)
vagyis
| \(\displaystyle (6)\) | \(\displaystyle a_0=\frac{m+M}{m}\frac{1}{\cos\alpha}A.\) |
A téglatest \(\displaystyle t\) idő alatt érkezik \(\displaystyle \frac h{\sin\alpha}-a=1~\)m-t megtéve lejtő aljára, vagyis
| \(\displaystyle (7)\) | \(\displaystyle \frac h{\sin\alpha}-a=\frac{a_0}{2}t^2.\) |
Az energiamegmaradás tétele szerint
\(\displaystyle \frac{1}{2}MV^2+\frac{1}{2}mu^2=mgh,\)
tehát
\(\displaystyle \frac{1}{2}M(At)^2+\frac{1}{2}m\left( a_0^2+A^2-2a_0A\cos\alpha \right)t^2=mg\frac{a_0}{2}t^2\,\sin\alpha.\)
Innen egyszerűsítések és (6) felhasználása után az
\(\displaystyle MA^2+m\left(A^2+\frac{(M+m)^2}{m^2\cos^2\alpha}A^2-2A^2\frac{ M+m }{m}\right)= (M+m)gA \frac{\sin\alpha}{\cos\alpha},\)
vagyis az
\(\displaystyle A=\frac{\sin\alpha\,\cos\alpha}{(M/m)+\sin^2\alpha}g=1{,}89~ \frac{\rm m}{s^2}\)
eredményt kapjuk. Innen (6) szerint
| \(\displaystyle (8)\) | \(\displaystyle a_0= \frac{\sin\alpha }{(M/m)+\sin^2\alpha}\left(1+\frac Mm\right)g=6{,}54~ \frac{\rm m}{s^2}.\) |
\(\displaystyle b)\) A csúszás ideje (7) alapján
\(\displaystyle t=\sqrt{ \frac2{a_0}\left({\frac h{\sin\alpha}-a}\right)}=0{,}55~\rm s.\)
\(\displaystyle a)\) A lejtő sebessége a téglatest leérkezésekor
\(\displaystyle V=At=1{,}04~\frac{\rm m }{\rm s},\)
a téglatest sebessége pedig (\(\displaystyle a_0t=3{,}60~\rm m/s\) ismeretében) (5) szerint
\(\displaystyle u=\sqrt{3{,}60^2+1{,}04^2-2\cdot3{,}60\cdot1{,}04\cdot\cos 30^\circ }~\frac{\rm m }{\rm s}=2{,}75~\frac{\rm m }{\rm s}. \)
\(\displaystyle c)\) A téglatest (a talajhoz képest)
\(\displaystyle \ell=\frac{u}{2}t=0{,}76~\rm m\)
utat tesz meg.
Statistics:
56 students sent a solution. 5 points: Csapó Tamás, Fey Dávid, Gurzó József, Kertész Balázs, Koleszár Benedek, Somlán Gellért, Toronyi András, Varga Vázsony, Viczián Máté. 4 points: Biebel Botond, Bubics Gergely Dániel, Horváth 999 Anikó, Kozaróczy Csaba, Ludányi Levente, Téglás Panna, Tóth Ábel, Török 111 László. 3 points: 8 students. 2 points: 16 students. 1 point: 6 students. 0 point: 7 students. Unfair, not evaluated: 2 solutionss.
Problems in Physics of KöMaL, December 2020
