 Problem P. 5274. (December 2020)
Problem P. 5274. (December 2020)
P. 5274. A rigid rod of length \(\displaystyle 3L\), shown in the figure can be rotated frictionlessly in a vertical plane about a horizontal axle, which is at a distance of \(\displaystyle L\) from the left end of the rod. The mass of the rod is negligible. Two small objects of masses \(\displaystyle m\) and \(\displaystyle 2m\) are attached to the ends of the rod, and the rod is held horizontally. Then the rod is released at a certain moment.
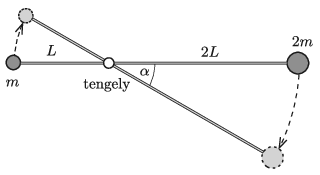
\(\displaystyle a)\) What is the magnitude of that component of the force exerted on the axle by the rod which is parallel to the rod at the moment when the angle between the rod and the horizontal is \(\displaystyle \alpha\)?
\(\displaystyle b)\) Determine the angle of \(\displaystyle \alpha\) at the moment when the magnitude of the total force exerted by the rod on the axle is \(\displaystyle 4mg\).
(5 pont)
Deadline expired on January 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) A két testből és az elhanyagolható tömegű rúdból álló rendszernek a tengelyre vonatkoztatott tehetetlenségi nyomatéka
\(\displaystyle \Theta=mL^2+(2m)(2L)^2=9mL^2.\)
A rúd \(\displaystyle \alpha\) szögű elfordulásakor a szögsebesség (az energiamegmaradás tétele szerint) így számolható:
\(\displaystyle \frac{1}{2}\Theta\omega^2=(2mg)(2L)\sin\alpha-mgL\sin\alpha,\)
vagyis
\(\displaystyle \omega=\sqrt{\frac{2}{3}\frac{g}{L}\sin\alpha}.\)
Jelöljük a \(\displaystyle m\) tömegű testre a rúd által kifejtett erő rúd irányú komponensét \(\displaystyle F_1\)-gyel, a másik testnél az ennek megfelelő erőt \(\displaystyle F_2\)-vel (1. ábra).
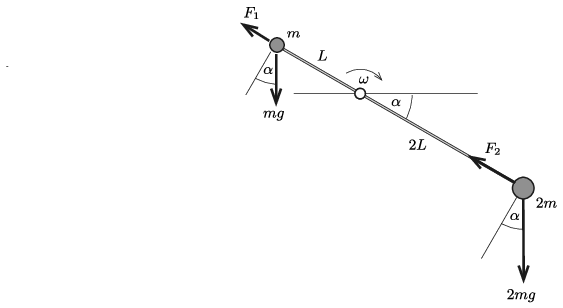
1. ábra
A mozgásegyenletek:
\(\displaystyle mg\sin\alpha-F_1=mL\omega^2,\)
ahonnan
\(\displaystyle F_1=\frac{1}{3}mg\sin\alpha,\)
illetve
\(\displaystyle F_2-2mg\sin\alpha=2m(2L)\omega^2,\)
vagyis
\(\displaystyle F_2=\frac{14}{3}mg\sin\alpha.\)
A tengelyre kifejtett rúdirányú erő ( a \(\displaystyle m\) tömegű test felé)
\(\displaystyle N_1=F_1+F_2=5mg\sin\alpha.\)
\(\displaystyle b)\) A testek nemcsak a rúd irányába, hanem arra merőlegesen is gyorsulnak. Ezt a tangenciális gyorsulást a nehézségi erőnek a rúdra merőleges komponense és a rúd által a rúdra merőleges irányban kifejtett \(\displaystyle F_3\) és \(\displaystyle F_4\) erő hozza létre (2. ábra).
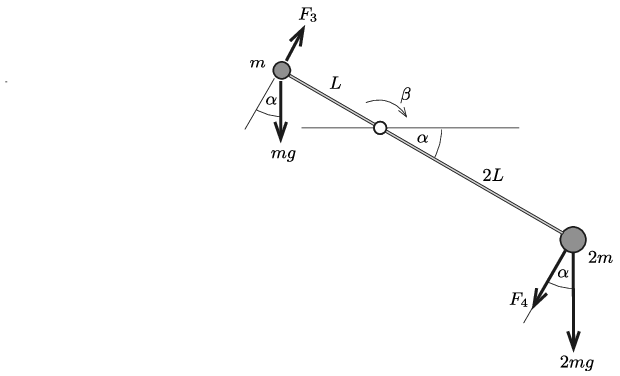
2. ábra
A mozgásegyenletek:
| \(\displaystyle (1)\) | \(\displaystyle F_3-mg\cos\alpha=mL\beta\) |
és
| \(\displaystyle (2)\) | \(\displaystyle 2mg\cos\alpha+F_4=2m(2L)\beta,\) |
ahol az egész merev test szöggyorsulása a külső erők eredő forgatónyomatékából számítható ki:
\(\displaystyle \beta=\frac{2mg(2L)\cos\alpha-mgL\cos\alpha}{\Theta}=\frac{1}{3}\frac{g}{L}\cos\alpha.\)
Ezt a kifejezést visszahelyettesítva (1)-be és (2)-be, kapjuk, hogy
\(\displaystyle F_3=\frac{4}{3}mg\cos\alpha, \qquad \text{illetve}\qquad F_4=-\frac{2}{3}mg\cos\alpha.\)
A tengelyre ható erőnek a rúdra merőleges összetevője:
\(\displaystyle N_2=F_3-F_4=2mg\cos\alpha.\)
A tengelyre ható teljes (eredő) erő
\(\displaystyle \vert\boldsymbol N\vert=\sqrt{N_1^2+N_2^2}=mg\sqrt{25\sin^2\alpha+4\cos^2\alpha}=mg\sqrt{21\sin^2\alpha+4},\)
ami akkor egyezik meg \(\displaystyle 4mg\)-vel, amikor
\(\displaystyle \sin^2\alpha=\frac{12}{21},\qquad \text{azaz}\qquad\alpha=\arcsin\sqrt{\frac{12}{21}}=49{,}1^\circ.\)
Statistics:
46 students sent a solution. 5 points: Gurzó József, Horváth Antal, Kertész Balázs, Kozák Gergely, Ludányi Levente, Molnár-Szabó Vilmos, Somlán Gellért, Téglás Panna. 4 points: Fekete András Albert, Nemeskéri Dániel, Sas 202 Mór. 3 points: 15 students. 2 points: 8 students. 1 point: 7 students. 0 point: 4 students. Unfair, not evaluated: 1 solutions.
Problems in Physics of KöMaL, December 2020
