 Problem P. 5314. (March 2021)
Problem P. 5314. (March 2021)
P. 5314. A vertical thermally insulated cylinder of cross sectional area \(\displaystyle A_0\) is open at its top and is divided into two parts by a thermally insulated piston of negligible width and mass. The part below the piston has a height of \(\displaystyle 2h_0\) and contains air. Above the piston there is some liquid of density \(\displaystyle \varrho\) and of height \(\displaystyle 2h_0\). Above the piston at a height of \(\displaystyle h_0\) a small hole of cross section \(\displaystyle A_1\) is opened at the beginning of the process, through which the liquid begins to flow out. The ambient atmospheric pressure is \(\displaystyle p_0=\varrho gh_0\).
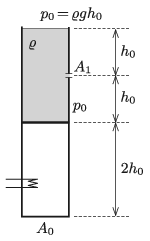
\(\displaystyle a)\) How should we change the power of the electric heating element which can heat the air below the piston in order that the fluid flow out at a constant rate?
\(\displaystyle b)\) For how long can we use the heating element to maintain the constant flow rate of the fluid, and after this time has elapsed why can't this be done with operating the heating element?
(6 pont)
Deadline expired on April 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A folyadék kiáramlási sebessége a lyuk feletti folyadékoszlop magasságától függ. Mivel a lyuk mérete kellően kicsi a henger alapterületéhez képest, kezdetben ez a kiáramlási sebesség:
\(\displaystyle v_0=\sqrt{2gh_0}.\)
A feladat szövege szerint úgy szeretnénk üzemeltetni a fűtőszálat, hogy ez a kiáramlási sebesség állandó értékű maradjon. Ez csak úgy lehetséges, ha a folyamat során nem változik a folyadékszint magassága a hengerben, vagyis a dugattyú annyival emeli meg a folyadékszintet, mint amennyivel az a kiáramlás miatt lesüllyedne. Ezt kihasználva fel lehet írni az elzárt levegő térfogat–idő függvényét. Egy rövid \(\displaystyle \Delta t\) idő alatt a kiáramló folyadék mennyisége:
\(\displaystyle \Delta V=A_1v_0\Delta t=A_1\sqrt{2gh_0}\Delta t.\)
Ha a folyadékszint magassága nem változik, akkor az elzárt levegőnek éppen ezzel az értékkel nő a térfogata. Mivel a térfogatváltozás állandó ütemű, így felírható a hengerben lévő levegő pillanatnyi térfogatának időbeli változása is:
\(\displaystyle V(t)=2h_0A_0+A_1\sqrt{2gh_0}t=A_0h_0\left(2+\frac{A_1}{A_0}\sqrt{\frac{2g}{h_0}}\,t\right).\)
Célszerű bevezetni a
\(\displaystyle V_0=A_0h_0\qquad \text{és} \qquad \frac{1}{t_0}=\frac{A_1}{A_0}\sqrt{\frac{2g}{h_0}}\)
jelöléseket. Ezekkel kifejezve a levegő térfogatának időbeli változását:
| \(\displaystyle (1)\) | \(\displaystyle V(t)=V_0\left(2+\frac{t}{t_0}\right).\) |
Ezek szemléletes jelentése:
\(\displaystyle V_0\) a kifolyónyílás feletti folyadékrész térfogata,
\(\displaystyle t_0\) az az idő, amennyi alatt az emelkedő dugattyú egyenletes mozgással elérné a kifolyónyílás szintjét.
A következő meghatározandó állapotjelző a levegő nyomása, annak időbeli változása. Mivel a dugattyú tömege elhanyagolható, így az egyensúlyának feltétele az, hogy a bezárt levegő nyomásából származó erő a felette elhelyezkedő folyadék hidrosztatikai nyomásával tartson egyensúlyt:
\(\displaystyle p(t)=p_0+\varrho g h(t),\)
ahol \(\displaystyle h(t)\) a folyadékoszlop pillanatnyi magassága. Ez a magasság a gáz térfogatának ismeretében így számolható:
\(\displaystyle h(t)=4h_0- \frac{{V(t)}}{A_0}.\)
A nyomás tehát
| \(\displaystyle (2) \) | \(\displaystyle p(t)=p_0\left(3-\frac{t}{t_0}\right).\) |
Megjegyzés. Ezt az eredményt úgy is megkaphatjuk, hogy meggondoljuk: kezdetben a gáz nyomása a külső légnyomás (\(\displaystyle p_0\)) és a \(\displaystyle 2h_0\) magas folyadékoszlop \(\displaystyle 2p_0\) hidrosztatikai nyomásának összege, tehát \(\displaystyle 3p_0\), továbbá az időben egyenletesen változó hidrosztatikai nyomás \(\displaystyle t_0\) idő alatt csökkenne \(\displaystyle p_0\)-lal.
\(\displaystyle a)\) Kicsiny \(\displaystyle \Delta t\) idő alatt a levegővel (melyre \(\displaystyle f=5\)) közlendő hő a hőtan első főtétele szerint:
\(\displaystyle \Delta Q=\frac{f}{2}\Delta (pV)+p\Delta V=\frac{7}{2}p\Delta V+\frac{5}{2}V\Delta p.\)
Az (1) és (2) összefüggések felhasználásával \(\displaystyle \Delta V=(V_0/t_0)\Delta t\), illetve \(\displaystyle \Delta p=-(p_0/t_0)\Delta t\). Ezek szerint a fűtőszál teljesítménye
\(\displaystyle P(t)=\frac{\Delta Q}{\Delta t}=\frac{p_0V_0}{2t_0}\left(11-12\frac{t}{t_0}\right).\)
Látjuk, hogy a fűtőszál teljesítményét időben egyenletesen csökkentenünk kell, ha az állandó kiáramlási sebességet fenn akarjuk tartani.
\(\displaystyle b)\) Azt is látjuk, hogy \(\displaystyle t^*=\frac{11}{12}t_0\) idő elteltével a teljesítmény már nullára csökken. A továbbiakban hűteni kellene a gázt, erre a fűtőszál nyilván nem képes, tehát a folyamat ,,megszalad''.
Megjegyzés. A továbbiakban a gáz állapotát a \(\displaystyle p-V\) diagramon szemléltető pont letér a lineáris szakaszról, és az adiabata mentén halad tovább. Anélkül, hogy hőt közölnénk a rendszerrel, a levegő térfogata nő, a nyomása és a hőmérséklete csökken. A nyomás csökkenése azonban nem olyan ütemű, mint amennyi a folyadékszint változatlan magasságban tartásához elegendő lenne, tehát a hengerben a folyadékszint ugrásszerűen emelkedni fog, a rendszer gejzírszerű viselkedésbe kezd.
Ellenőriznünk kell még, hogy \(\displaystyle t=t^*\) időpontig (vagy még előtte) nem éri-e el a dugattyú a kifolyónyílást. Mivel \(\displaystyle t^*<t_0\),
\(\displaystyle V(t^*)=\left(2+\frac{11}{12}\right)V_0\approx 2{,}92\,V_0<3\,V_0,\)
a dugattyú még éppen a kifolyónyílás alatt maradt. Érdekes, hogy a \(\displaystyle p(t)\cdot V(t)\)-vel arányos hőmérséklet a melegítés során a \(\displaystyle t=\tfrac12 t_0\) időpillanatban éri el a maximális értékét, ettől kezdve a levegő – jóllehet a fűtőszállal fűtjük – hűl!
Statistics:
17 students sent a solution. 6 points: Kertész Balázs, Somlán Gellért, Téglás Panna, Toronyi András. 5 points: Fekete András Albert, Gurzó József, Selmi Bálint. 4 points: 1 student. 3 points: 3 students. 2 points: 1 student. 1 point: 3 students. 0 point: 2 students.
Problems in Physics of KöMaL, March 2021
