A P. 5329. feladat (2021. május)

P. 5329. Vízszintes táblán egy krétadarab nyugszik. A táblát meglökve, a tábla hirtelen vízszintes, \(\displaystyle v_0\) nagyságú sebességet kap, majd \(\displaystyle T\) idő múlva egy falnak ütközve ugyanilyen hirtelen megáll. Milyen hosszú nyomot hagy a kréta a táblán, ha a kréta és a tábla közötti súrlódási együttható \(\displaystyle \mu\)?

A Kvant nyomán

(5 pont)

A beküldési határidő 2021. június 15-én LEJÁRT.

Megoldás. A tábla hirtelen megindításakor a kréta sebessége még nulla, a tábláé \(\displaystyle v_0\). Ezután a kréta sebessége a \(\displaystyle \mu m g\) súrlódási erő miatt \(\displaystyle a=\mu g\) gyorsulásnak megfelelő ütemben növekszik mindaddig, amíg a relatív sebességük nullára nem csökken, vagy a relatív sebesség előjele meg nem változik.

A továbbiakban két esetet kell megkülönböztetnünk:

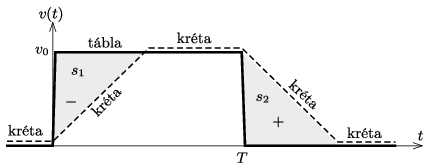
\(\displaystyle a)\) Ha \(\displaystyle v_0/(\mu g)\le T\), akkor a kréta \(\displaystyle t_1= v_0/(\mu g)\) idő múlva (a táblához képest) megáll, miközben az elmozdulása a táblán (vagyis a krétanyom ,,előjeles hossza'')

\(\displaystyle s_1=-\frac{1}{2}v_0 t_1= -\frac{v_0^2}{2\mu g}.\)

(A negatív előjel azt fejezi ki, hogy a kréta lemarad a táblától.) A tábla későbbi – ugyancsak hirtelen – megállításakor a kréta sebessége \(\displaystyle +v_0\), további mozgását pedig \(\displaystyle a=-\mu g\) lassulás jellemzi. A kréta sebessége

\(\displaystyle v(t)=v_0-\mu g t\)

módon változik, és a megállásig

\(\displaystyle s_2=+\frac{v_0^2}{2\mu g}\)

utat tesz meg. A krétanyom látható hossza

\(\displaystyle s=s_1=\frac{v_0^2}{2\mu g},\)

hiszen a táblához képest előrefelé mozgó kréta csak vastagítja a már meglévő nyomot, de annak hosszát nem növeli (1. ábra).

1. ábra

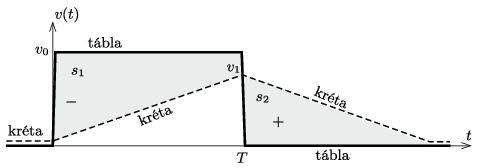
\(\displaystyle b)\) Amennyiben \(\displaystyle v_0/(\mu g)> T\), a kréta sebessége a tábla megindulása után \(\displaystyle T\) idő elteltével \(\displaystyle v_1=\mu g T<v_0.\) Ezalatt a kréta

\(\displaystyle s_1= \frac{v_0+\left(v_0-v_1\right)}{2}T=v_0T-\frac{\mu g}{2}T^2\)

hosszú nyomot hagy a táblán. A tábla hirtelen megállítása után a kréta sebessége a \(\displaystyle v_1\) kezdeti értékről \(\displaystyle T\) idő alatt nullára csökken, vagyis

\(\displaystyle s_2=\frac{v_1}{2}T\)

hosszú nyomot húz a táblán az előző nyommal ellentétes irányban (2. ábra). Mivel \(\displaystyle s_1>s_2,\) a teljes krétanyom hossza

\(\displaystyle s=s_1=v_0T-\frac{\mu g}{2}T^2.\)

2. ábra

Statisztika:

17 dolgozat érkezett.
5 pontot kapott:	Gábriel Tamás, Hauber Henrik, Juhász Márk Hunor, Kertész Balázs, Koleszár Benedek, Köpenczei Csanád, Ludányi Levente, Somlán Gellért, Toronyi András, Tóth Ábel, Varga Vázsony.
4 pontot kapott:	Bonifert Balázs.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2021. májusi fizika feladatai