 Problem P. 5332. (May 2021)
Problem P. 5332. (May 2021)
P. 5332. A small ball of mass \(\displaystyle m\) and of charge \(\displaystyle Q=1~\mu\)C hangs on a piece of insulating thread of length \(\displaystyle L = 0.2\) m. At a distance of \(\displaystyle 2L\) below the suspension there is another small fixed ball of charge \(\displaystyle Q\).
\(\displaystyle a)\) How does the angle between the thread and the vertical depend on the mass \(\displaystyle m\)?
\(\displaystyle b)\) What should the least value of \(\displaystyle m\) be in order to have a distance of \(\displaystyle L\) between the two balls?
\(\displaystyle c)\) What should the maximum value of \(\displaystyle m\) be in order to have a distance of \(\displaystyle 3L\) between the two balls?
(5 pont)
Deadline expired on June 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) Ha a fonál \(\displaystyle \alpha\) szöget zár be a függőlegessel, akkor a töltések távolsága (a koszinusztétel szerint)
| \(\displaystyle (1)\) | \(\displaystyle d=\sqrt{(2L)^2+L^2-2L\cdot L\cdot \cos\alpha}=L\sqrt{5-4\cos \alpha}.\) |
A két töltés között ható (taszító) Coulomb-erő nagysága:
| \(\displaystyle (2)\) | \(\displaystyle F(\alpha)=k\frac{Q^2}{d^2},\) |
a nehézségi erő pedig
| \(\displaystyle (3)\) | \(\displaystyle G=mg.\) |
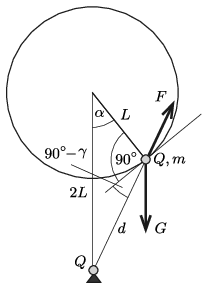
1. ábra
A felfüggesztett golyócska akkor lehet egyensúlyban, ha \(\displaystyle \boldsymbol F\) és \(\displaystyle \boldsymbol G\) eredője a fonál irányába mutat, vagyis ezen két erőnek a fonálra merőleges (érintő irányú) komponense egyforma nagyságú. Az 1. ábrán látható jelölésekkel az egyensúly feltétele:
\(\displaystyle G\,\sin\alpha=F\,\cos(\gamma-90^\circ),\)
vagyis
| \(\displaystyle (4)\) | \(\displaystyle G\,\sin\alpha=F\,\sin\gamma.\) |
Az ábrán látható háromszögre felírható szinusztétel szerint
\(\displaystyle \frac{\sin\gamma}{\sin\alpha}=\frac{2L}{d},\)
és így az egyensúly (4) feltétele:
| \(\displaystyle (5)\) | \(\displaystyle mg\cdot\sin\alpha=k\frac{2Q^2L}{d^3}\cdot\sin\alpha.\) |
Az \(\displaystyle \alpha=0\) helyzethez tartozó elektrosztatikus erő és a nehézségi erő hányadosára érdemes bevezetni a
| \(\displaystyle (6)\) | \(\displaystyle \lambda=k\frac{Q^2}{L^2mg}\) |
dimenziótlan mennyiséget. Ennek segítségével az (5) egyensúlyi egyenlet:
| \(\displaystyle (7)\) | \(\displaystyle \sin\alpha\, \left(2\lambda\frac{L^3}{d^3}-1\right)=0.\) |
Az \(\displaystyle \alpha=0\) és \(\displaystyle \alpha=180^\circ\) helyzetek nyilván egyensúlyi állapotok, azonban ezek – a töltések és a tömeg nagyságától függően – lehetnek stabil vagy instabil egyensúlyi helyzetek. Emellett figyelembe kell vegyük azt is, hogy \(\displaystyle \lambda>1\) esetén az legalsó (\(\displaystyle \alpha=0\)) helyzetben a fonál meglazul, és ugyanez történik \(\displaystyle \lambda<9\) esetén az \(\displaystyle \alpha=180^\circ\)-os felső helyzetben.
További egyensúlyi helyzetek is lehetségesek, ha a (7)-ben szerepló zárójeles tényező válik nullává, vagyis ha (1)-et felhasználva teljesül, hogy
\(\displaystyle 2\lambda\left(5-4\cos\alpha\right)^{- {3}/{2}}=1,\)
azaz
| \(\displaystyle (8)\) | \(\displaystyle \cos\alpha=\frac{5-(2\lambda)^{2/3}}{4}.\) |
Mivel \(\displaystyle -1\le\cos\alpha\ge 1\), (8)-nak csak akkor van megoldása, ha
\(\displaystyle \frac{1}{2}\le\lambda\le \frac{27}{2}.\)
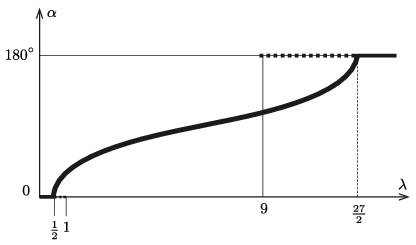
2. ábra
A 2. ábra a lehetséges egyensúlyi helyzetekhez tartozó szögeket mutatja a \(\displaystyle \lambda\) paraméter (ami kifejezhető az \(\displaystyle m\) tömeggel) függvényében. A folytonos (vastag) vonal a stabil, a szaggatott vonal pedig az instabil állapotat jelzi. (Az instabil állapotok vonala a fonál meglazulása miatt szakad meg \(\displaystyle \lambda=1\) és \(\displaystyle \lambda=9\) értékeknél.)
\(\displaystyle b)\) Ha \(\displaystyle \lambda\le \frac12\), vagyis
\(\displaystyle m\ge \frac{2kQ^2}{L^2g}=\frac{2\cdot\cdot9\cdot10^9\cdot 10^{-12}}{0{,}04\cdot 9{,}81}~{\rm kg}\approx 46~\rm g,\)
akkor \(\displaystyle \alpha=0\), tehát a két golyó távolsága \(\displaystyle L\) marad.
\(\displaystyle c)\) Ha \(\displaystyle \lambda\ge \frac{27}2\), vagyis
\(\displaystyle m\le \frac{2\,kQ^2}{27\,L^2g}\approx 1{,}7~\rm g,\)
akkor \(\displaystyle \alpha=180^\circ\), tehát a két golyó távolsága \(\displaystyle 3L\) lesz.
Statistics:
21 students sent a solution. 5 points: Antalóczy Szabolcs, Biebel Botond, Gábriel Tamás, Kertész Balázs, Mozolai Bende Bruno, Téglás Panna, Toronyi András. 4 points: Kovács Kinga, Varga Vázsony. 3 points: 4 students. 2 points: 5 students. 1 point: 2 students. 0 point: 1 student.
Problems in Physics of KöMaL, May 2021
