 |
A P. 5336. feladat (2021. május) |
P. 5336. Elég nagy kiterjedésű, széles, sík mező fölött 2 km magasan repül egy szuperszonikus vadászgép vízszintes irányban. A gép hangját a mezőn álló három, egymástól páronként 14 km-re lévő megfigyelő egyszerre hallja meg. A repülőgép éppen az egyik megfigyelő feje felett repül el. Mekkora a vadászgép sebessége?
Közli: Vigh Máté, Biatorbágy
(6 pont)
A beküldési határidő 2021. június 15-én LEJÁRT.
I. megoldás. A \(\displaystyle H=2\) km magasságban \(\displaystyle v\) sebességgel haladó vadászgép \(\displaystyle c\) sebességű hangterjedés (\(\displaystyle v>c\)) esetén egy olyan \(\displaystyle \alpha\) félnyílásszögű kúpot (ún. Mach-kúpot) ,,húz maga után'', amelyre teljesül, hogy
\(\displaystyle \frac{c}{v}=\sin\alpha.\)
A Mach-kúp felületének pontjaiba egyszerre érkezik meg a repülőgép hangja. A Mach-kúp és a vízszintes, sík mező közös pontjai egy olyan hiperbolán helyezkednek el, amelynek aszimptotái \(\displaystyle 2\alpha\) szöget zárnak be egymással, és a hiperbola két ágának távolsága \(\displaystyle 2H\,\ctg\alpha\) (1. ábra).
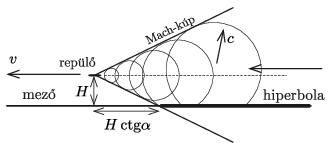
1. ábra
Három megfigyelő akkor hallja meg egyszerre a repülőgép hangját, ha az általuk meghatározott \(\displaystyle L=14~\)km oldalélű, szabályos háromszög illeszkedik a hiperbolára. Mivel a gép éppen az egyik (\(\displaystyle A\)-val jelölt) megfigyelő feje felett repül el, a gép pályájának vetülete a mezőn (ami a hiperbola egyik tengelye) áthalad az \(\displaystyle A\) ponton. A másik két megfigyelő erre a tengelyre szimmetrikusan helyezkedik el, hiszen az \(\displaystyle A\)-tól mért távolságuk ugyanakkora (2. ábra).
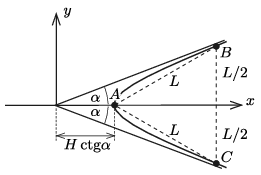
2. ábra
A három megfigyelő koordinátái:
\(\displaystyle A: \qquad (H\,\ctg\alpha, 0),\)
\(\displaystyle B: \qquad \left( \ctg\alpha\sqrt{\left(\frac{L}{2}\right)^2+H^2}, \frac{L }{2}\right),\)
\(\displaystyle C: \qquad \left( \ctg\alpha\sqrt{\left(\frac{L}{2}\right)^2+H^2}, -\frac{L }{2}\right).\)
Az adatok behelyettesítése után ezt kapjuk:
\(\displaystyle \ctg\alpha(\sqrt{53}-2)+7^2=14^2,\)
ahonnan
\(\displaystyle \tg\alpha=0{,}435 \qquad \Rightarrow \qquad \alpha=23{,}5^\circ,\)
tehát
\(\displaystyle M=\frac{v}{c}=\frac{1}{\sin\alpha}\approx 2{,}5.\)
A repülőgép tehát 2,5 mach-hal (vagyis a hangsebesség 2,5-szörösével), mintegy 3060 km/h sebességgel repült.
II. megoldás. Képzeljük magunkat az egyik megfigyelő helyébe. A tőlünk \(\displaystyle H\) távolságban lévő egyenes mentén a repülő \(\displaystyle v\) sebességgel mozog, a kibocsátott hang pedig \(\displaystyle c\) \(\displaystyle (c<v)\) sebességgel. Az, hogy a repülő különböző időpillanatokban kibocsátott hangja mikor érkezik legelőször hozzánk, a repülő távolságától és a sebességének felénk mutató \(\displaystyle v_r\) (radiális) komponensétől függ. Mindaddig, amíg \(\displaystyle v_r>c\), a repülő ,,lehagyja'' a hangját. Hozzánk az a hang érkezik meg legelőször, ami a \(\displaystyle v_r=c\) egyenlőségnek megfelelő helyről indult ki, vagyis amikor a fokozatosan csökkenő radiális sebességkomponens átlépi a hangsebességet. (Ilyenkor a hozzánk érkező hang intenzitása is lényegesen megnő, ezért érzékelünk ,,hangrobbanást''.)
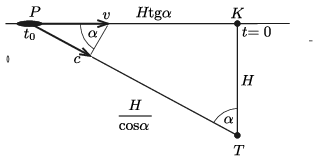
3. ábra
Válasszuk az időmérés kezdőpontját úgy, hogy a repülőgép éppen a ,,fejünk felett'' (a hozzánk legközelebbi pontban) legyen \(\displaystyle t=0\). Számítsuk ki, hogy mikor (milyen \(\displaystyle T\) időpontban) érkezik hozzánk először a hang. A 3. ábráról leolvashatjuk, hogy a hangsebesség átlépése annál a \(\displaystyle P\) pontnál következik be, amely a röppálya hozzánk legközelebbi \(\displaystyle K\) pontjába mutató egyenessel bezárt szögre
\(\displaystyle \sin\alpha=\frac{c}{v}\)
teljesül. Mivel a \(\displaystyle PK\) távolság \(\displaystyle H\tg\alpha\), a \(\displaystyle P\) pontba
\(\displaystyle t_0=-\frac{H}{v}\tg\alpha\)
időpillanatban érkezik a repülőgép. Innen a hangnak \(\displaystyle \frac{H}{\cos\alpha}\) utat kell még megtennie, hogy hozzánk érkezzen, így
| \(\displaystyle (1)\) | \(\displaystyle T=t_0+\frac{H}{c\cos\alpha}=\frac{H}{c\cos\alpha}-\frac{H\tg\alpha}{v}= \frac{H}{v}\left(\frac{1}{\sin\alpha\,\cos\alpha}-\frac{\sin\alpha}{\cos\alpha}\right)=\frac{H}{v}\ctg\alpha.\) |
Tekintsük a szabályos háromszög csúcsaiban elhelyezkedő három megfigyelőt ,,felülről'' nézve (4. ábra). (A távolságokat kilométer egységekben mérjük.) Feltehetjük, hogy a repülő az \(\displaystyle A\) ponthoz tartozó magasságvonal felett repül el \(\displaystyle H=2\) km magasságban. A hangja (1) szerint
\(\displaystyle T_A=\frac{2}{v}\ctg\alpha\)
időpontban érkezik az \(\displaystyle A\) megfigyelőhöz.
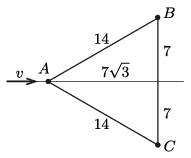
4. ábra
A \(\displaystyle B\) és \(\displaystyle C\) megfigyelők a repülőgép pályájától
\(\displaystyle H'=\sqrt{7^2+2^2}= \sqrt{53}\)
egység távolságra vannak, hozzájuk tehát
\(\displaystyle T_B=T_C=\frac{\sqrt{53}}{v}\ctg\alpha-\frac{ 7\sqrt{3}}{v} \)
időpontban érkezik meg a legelső hang. (A képlet jobb oldalának második tagja azt veszi figyelembe, hogy a repülőgépnek \(\displaystyle v\) sebességgel meg kell tennie az \(\displaystyle A\) és \(\displaystyle B\)-hez legközelebbi helyzeteknek megfelelő \(\displaystyle 7\sqrt{3}\) km-nyi távolságot.)
A \(\displaystyle T_A=T_B=T_C\) feltétel akkor teljesül, ha
\(\displaystyle 2\ctg\alpha=\sqrt{53}\ctg\alpha-7\sqrt{3},\)
vagyis
\(\displaystyle \ctg\alpha=\frac{7\sqrt{3}}{\sqrt{53}-2}=2{,}29,\)
ahonnan \(\displaystyle \alpha =23{,}5^\circ,\) vagyis
\(\displaystyle \frac{v}{c}=\frac{1}{\sin\alpha}\approx 2{,}5.\)
Statisztika:
9 dolgozat érkezett. 6 pontot kapott: Kertész Balázs, Somlán Gellért, Téglás Panna, Tóth Ábel, Varga Vázsony. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2021. májusi fizika feladatai

