 Problem P. 5336. (May 2021)
Problem P. 5336. (May 2021)
P. 5336. A supersonic fighter-plane flies 2 km above a fairly large, wide, flat field along a horizontal line. The sound of the fighter is heard at the same instant by three observers standing in the field, 14 km apart pairwise. The fighter is right above the head of one of the observers. What is the speed of the fighter?
(6 pont)
Deadline expired on June 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. A \(\displaystyle H=2\) km magasságban \(\displaystyle v\) sebességgel haladó vadászgép \(\displaystyle c\) sebességű hangterjedés (\(\displaystyle v>c\)) esetén egy olyan \(\displaystyle \alpha\) félnyílásszögű kúpot (ún. Mach-kúpot) ,,húz maga után'', amelyre teljesül, hogy
\(\displaystyle \frac{c}{v}=\sin\alpha.\)
A Mach-kúp felületének pontjaiba egyszerre érkezik meg a repülőgép hangja. A Mach-kúp és a vízszintes, sík mező közös pontjai egy olyan hiperbolán helyezkednek el, amelynek aszimptotái \(\displaystyle 2\alpha\) szöget zárnak be egymással, és a hiperbola két ágának távolsága \(\displaystyle 2H\,\ctg\alpha\) (1. ábra).
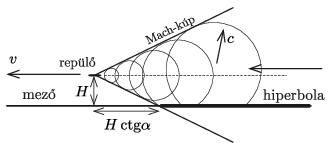
1. ábra
Három megfigyelő akkor hallja meg egyszerre a repülőgép hangját, ha az általuk meghatározott \(\displaystyle L=14~\)km oldalélű, szabályos háromszög illeszkedik a hiperbolára. Mivel a gép éppen az egyik (\(\displaystyle A\)-val jelölt) megfigyelő feje felett repül el, a gép pályájának vetülete a mezőn (ami a hiperbola egyik tengelye) áthalad az \(\displaystyle A\) ponton. A másik két megfigyelő erre a tengelyre szimmetrikusan helyezkedik el, hiszen az \(\displaystyle A\)-tól mért távolságuk ugyanakkora (2. ábra).
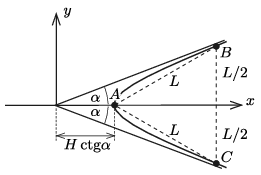
2. ábra
A három megfigyelő koordinátái:
\(\displaystyle A: \qquad (H\,\ctg\alpha, 0),\)
\(\displaystyle B: \qquad \left( \ctg\alpha\sqrt{\left(\frac{L}{2}\right)^2+H^2}, \frac{L }{2}\right),\)
\(\displaystyle C: \qquad \left( \ctg\alpha\sqrt{\left(\frac{L}{2}\right)^2+H^2}, -\frac{L }{2}\right).\)
Az adatok behelyettesítése után ezt kapjuk:
\(\displaystyle \ctg\alpha(\sqrt{53}-2)+7^2=14^2,\)
ahonnan
\(\displaystyle \tg\alpha=0{,}435 \qquad \Rightarrow \qquad \alpha=23{,}5^\circ,\)
tehát
\(\displaystyle M=\frac{v}{c}=\frac{1}{\sin\alpha}\approx 2{,}5.\)
A repülőgép tehát 2,5 mach-hal (vagyis a hangsebesség 2,5-szörösével), mintegy 3060 km/h sebességgel repült.
II. megoldás. Képzeljük magunkat az egyik megfigyelő helyébe. A tőlünk \(\displaystyle H\) távolságban lévő egyenes mentén a repülő \(\displaystyle v\) sebességgel mozog, a kibocsátott hang pedig \(\displaystyle c\) \(\displaystyle (c<v)\) sebességgel. Az, hogy a repülő különböző időpillanatokban kibocsátott hangja mikor érkezik legelőször hozzánk, a repülő távolságától és a sebességének felénk mutató \(\displaystyle v_r\) (radiális) komponensétől függ. Mindaddig, amíg \(\displaystyle v_r>c\), a repülő ,,lehagyja'' a hangját. Hozzánk az a hang érkezik meg legelőször, ami a \(\displaystyle v_r=c\) egyenlőségnek megfelelő helyről indult ki, vagyis amikor a fokozatosan csökkenő radiális sebességkomponens átlépi a hangsebességet. (Ilyenkor a hozzánk érkező hang intenzitása is lényegesen megnő, ezért érzékelünk ,,hangrobbanást''.)
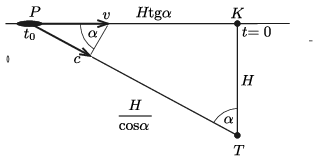
3. ábra
Válasszuk az időmérés kezdőpontját úgy, hogy a repülőgép éppen a ,,fejünk felett'' (a hozzánk legközelebbi pontban) legyen \(\displaystyle t=0\). Számítsuk ki, hogy mikor (milyen \(\displaystyle T\) időpontban) érkezik hozzánk először a hang. A 3. ábráról leolvashatjuk, hogy a hangsebesség átlépése annál a \(\displaystyle P\) pontnál következik be, amely a röppálya hozzánk legközelebbi \(\displaystyle K\) pontjába mutató egyenessel bezárt szögre
\(\displaystyle \sin\alpha=\frac{c}{v}\)
teljesül. Mivel a \(\displaystyle PK\) távolság \(\displaystyle H\tg\alpha\), a \(\displaystyle P\) pontba
\(\displaystyle t_0=-\frac{H}{v}\tg\alpha\)
időpillanatban érkezik a repülőgép. Innen a hangnak \(\displaystyle \frac{H}{\cos\alpha}\) utat kell még megtennie, hogy hozzánk érkezzen, így
| \(\displaystyle (1)\) | \(\displaystyle T=t_0+\frac{H}{c\cos\alpha}=\frac{H}{c\cos\alpha}-\frac{H\tg\alpha}{v}= \frac{H}{v}\left(\frac{1}{\sin\alpha\,\cos\alpha}-\frac{\sin\alpha}{\cos\alpha}\right)=\frac{H}{v}\ctg\alpha.\) |
Tekintsük a szabályos háromszög csúcsaiban elhelyezkedő három megfigyelőt ,,felülről'' nézve (4. ábra). (A távolságokat kilométer egységekben mérjük.) Feltehetjük, hogy a repülő az \(\displaystyle A\) ponthoz tartozó magasságvonal felett repül el \(\displaystyle H=2\) km magasságban. A hangja (1) szerint
\(\displaystyle T_A=\frac{2}{v}\ctg\alpha\)
időpontban érkezik az \(\displaystyle A\) megfigyelőhöz.
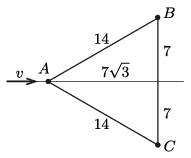
4. ábra
A \(\displaystyle B\) és \(\displaystyle C\) megfigyelők a repülőgép pályájától
\(\displaystyle H'=\sqrt{7^2+2^2}= \sqrt{53}\)
egység távolságra vannak, hozzájuk tehát
\(\displaystyle T_B=T_C=\frac{\sqrt{53}}{v}\ctg\alpha-\frac{ 7\sqrt{3}}{v} \)
időpontban érkezik meg a legelső hang. (A képlet jobb oldalának második tagja azt veszi figyelembe, hogy a repülőgépnek \(\displaystyle v\) sebességgel meg kell tennie az \(\displaystyle A\) és \(\displaystyle B\)-hez legközelebbi helyzeteknek megfelelő \(\displaystyle 7\sqrt{3}\) km-nyi távolságot.)
A \(\displaystyle T_A=T_B=T_C\) feltétel akkor teljesül, ha
\(\displaystyle 2\ctg\alpha=\sqrt{53}\ctg\alpha-7\sqrt{3},\)
vagyis
\(\displaystyle \ctg\alpha=\frac{7\sqrt{3}}{\sqrt{53}-2}=2{,}29,\)
ahonnan \(\displaystyle \alpha =23{,}5^\circ,\) vagyis
\(\displaystyle \frac{v}{c}=\frac{1}{\sin\alpha}\approx 2{,}5.\)
Statistics:
9 students sent a solution. 6 points: Kertész Balázs, Somlán Gellért, Téglás Panna, Tóth Ábel, Varga Vázsony. 3 points: 1 student. 2 points: 1 student. 1 point: 2 students.
Problems in Physics of KöMaL, May 2021
