 |
A P. 5338. feladat (2021. szeptember) |
P. 5338. A bal oldali ábrán látható módon egy dominópárt helyezünk el egy harmadikon.
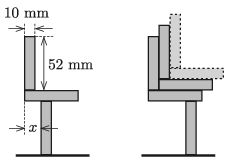
\(\displaystyle a)\) Határozzuk meg \(\displaystyle x\) lehetséges értékeit, hogy a dominók egyensúlyban legyenek.
\(\displaystyle b)\) Ezt követően további dominópárokat helyezünk el a jobb oldali ábrának megfelelően. Legfeljebb hány dominót helyezhetünk el a legalsóra, hogy az egyensúlyi állapot fennmaradjon?
Közli: Simon Péter, Pécs
(5 pont)
A beküldési határidő 2021. október 15-én LEJÁRT.
Megoldás. \(\displaystyle a)\) A felső két dominó tömegközéppontja a vízszintes helyzetű, \(\displaystyle m\) tömegű dominó bal szélétől vízszintes irányban mérve
\(\displaystyle s_1=\frac{m\cdot26~{\rm mm}+m\cdot5~{\rm mm}}{2m}=15{,}5~{\rm mm}\)
távol van. Ha \(\displaystyle x>s_1,\) akkor a felső két dominó balra dől, ha pedig \(\displaystyle x+10~{\rm mm}<s_1\), akkor jobbfelé billen a domonópár. Az egyensúly feltétele tehát:
\(\displaystyle 5{,}5~{\rm mm}<x<15{,}5~{\rm mm}.\)
\(\displaystyle b)\) Két dominópár tömegközéppontja az egész elrendezés bal szélétől
\(\displaystyle s_2=\frac{15{,}5+25{,}5}{2}~{\rm mm}=20{,}5~{\rm mm},\)
három dominópáré
\(\displaystyle s_3=\frac{15{,}5+25{,}5+35{,}5}{3}~{\rm mm}=25{,}5~{\rm mm},\)
és általában \(\displaystyle n\) dominópár tömegközéppontja az egész elrendezés bal szélétől
\(\displaystyle s_n=(10{,}5+ 5\cdot n)~{\rm mm}\)
távol található.
Az \(\displaystyle n\) dominópár akkor nem billen jobbra a függőlegesen álló ,,lábon'', ha
\(\displaystyle s_n<52~{\rm mm},\qquad \text{vagyis}\qquad n<8{,}3.\)
A felső \(\displaystyle n-1\) dominópár akkor nem billen el jobbra, ha
\(\displaystyle s_{n-1}<42~{\rm mm},\qquad \text{vagyis}\qquad n<7{,}3.\)
Ez erősebb feltétel, mint a teljes (\(\displaystyle 2n\) darabból álló) rendszer stabilitásának feltétele. Ha ez teljesül, akkor minden \(\displaystyle i<n-1\)-re \(\displaystyle s_i<42,\) tehát az építmény többi része sem borul le.
Megállapíthatjuk tehát, hogy legfeljebb 7 dominópár, azaz \(\displaystyle n_{\rm max}=14\) darab dominó helyezhető el a legalsóra.
Statisztika:
55 dolgozat érkezett. 5 pontot kapott: Szabó Márton. 4 pontot kapott: Bencz Benedek, Budai Csanád, Hauber Henrik, Hegedűs Tamás, Kertész Balázs, Köpenczei Csanád, Magyar Gábor Balázs, Molnár-Szabó Vilmos, Páhán Anita Dalma, Pethő Dorottya, Szanyi Attila, Török Eszter Júlia, Yokota Adan. 3 pontot kapott: 16 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 5 versenyző.
A KöMaL 2021. szeptemberi fizika feladatai

