 Problem P. 5338. (September 2021)
Problem P. 5338. (September 2021)
P. 5338. A pair of dominoes are placed to a third domino as it is shown in the left figure.
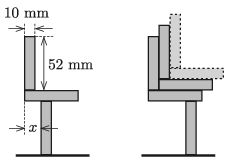
\(\displaystyle a)\) Determine the possible values of \(\displaystyle x\) such that the dominoes are in stable equilibrium.
\(\displaystyle b)\) Then several more domino pairs are placed to the dominoes as shown in the right figure. At most how many dominoes can be placed on the domino at the bottom in order that the system remain in equilibrium?
(5 pont)
Deadline expired on October 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) A felső két dominó tömegközéppontja a vízszintes helyzetű, \(\displaystyle m\) tömegű dominó bal szélétől vízszintes irányban mérve
\(\displaystyle s_1=\frac{m\cdot26~{\rm mm}+m\cdot5~{\rm mm}}{2m}=15{,}5~{\rm mm}\)
távol van. Ha \(\displaystyle x>s_1,\) akkor a felső két dominó balra dől, ha pedig \(\displaystyle x+10~{\rm mm}<s_1\), akkor jobbfelé billen a domonópár. Az egyensúly feltétele tehát:
\(\displaystyle 5{,}5~{\rm mm}<x<15{,}5~{\rm mm}.\)
\(\displaystyle b)\) Két dominópár tömegközéppontja az egész elrendezés bal szélétől
\(\displaystyle s_2=\frac{15{,}5+25{,}5}{2}~{\rm mm}=20{,}5~{\rm mm},\)
három dominópáré
\(\displaystyle s_3=\frac{15{,}5+25{,}5+35{,}5}{3}~{\rm mm}=25{,}5~{\rm mm},\)
és általában \(\displaystyle n\) dominópár tömegközéppontja az egész elrendezés bal szélétől
\(\displaystyle s_n=(10{,}5+ 5\cdot n)~{\rm mm}\)
távol található.
Az \(\displaystyle n\) dominópár akkor nem billen jobbra a függőlegesen álló ,,lábon'', ha
\(\displaystyle s_n<52~{\rm mm},\qquad \text{vagyis}\qquad n<8{,}3.\)
A felső \(\displaystyle n-1\) dominópár akkor nem billen el jobbra, ha
\(\displaystyle s_{n-1}<42~{\rm mm},\qquad \text{vagyis}\qquad n<7{,}3.\)
Ez erősebb feltétel, mint a teljes (\(\displaystyle 2n\) darabból álló) rendszer stabilitásának feltétele. Ha ez teljesül, akkor minden \(\displaystyle i<n-1\)-re \(\displaystyle s_i<42,\) tehát az építmény többi része sem borul le.
Megállapíthatjuk tehát, hogy legfeljebb 7 dominópár, azaz \(\displaystyle n_{\rm max}=14\) darab dominó helyezhető el a legalsóra.
Statistics:
55 students sent a solution. 5 points: Szabó Márton. 4 points: Bencz Benedek, Budai Csanád, Hauber Henrik, Hegedűs Tamás, Kertész Balázs, Köpenczei Csanád, Magyar Gábor Balázs, Molnár-Szabó Vilmos, Páhán Anita Dalma, Pethő Dorottya, Szanyi Attila, Török Eszter Júlia, Yokota Adan. 3 points: 16 students. 2 points: 9 students. 1 point: 7 students. 0 point: 5 students.
Problems in Physics of KöMaL, September 2021
