 Problem P. 5341. (September 2021)
Problem P. 5341. (September 2021)
P. 5341. A freight train carries a cuboid-shaped container of length \(\displaystyle \ell\), width \(\displaystyle d\) and height \(\displaystyle h\). The container is halfway filled with some liquid of density \(\displaystyle \varrho\). What force would the liquid exert on the base and each of the side faces of the container, if the train was able to move at a constant acceleration of \(\displaystyle a_0\) for a long time? (The longer edge of the container is parallel to the rails, and the liquid would not flow out of the container even if it was open at its top.)
Data: \(\displaystyle \ell=10\) m, \(\displaystyle h=d=3\) m, \(\displaystyle \varrho=1000~\mathrm{kg/m}^3\), \(\displaystyle a_0=1~\mathrm{m/s}^2\).
(5 pont)
Deadline expired on October 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Belátjuk, hogy a folyadék felszíne (amikor a folyadék a konténerhez képest már nem mozog) egy olyan sík, amelyik \(\displaystyle \alpha=\arctg(a_0/g)\) szöget zár be a vízszintessel. A folyadék felszínének közelében a folyadék egy kicsiny darabkájára a környező folyadék csak a felszínre merőleges \(\displaystyle F\) erőt képes kifejteni. (Ha nem így lenne, akkor a kérdéses anyagdarabka a felület érintősíkjában elmozdulna a folyadék többi részéhet képest.) Az 1. ábráról leolvasható, hogy egy \(\displaystyle m\) tömegű ,,folyadékdarabka'' mozgásegyenle a felület esésvonalának irányában
\(\displaystyle mg\sin\alpha=ma_0\cos\alpha,\qquad \text{tehát}\qquad \tg\alpha=\frac{a_0}{g}.\)
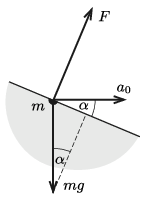
1. ábra
A gyorsulás következtében a konténer elején a folyadék magassága
\(\displaystyle h_1=\frac{h}{2}-\frac{\ell}{2}\,\frac{a_0}{g}\)
értékre csökken, a konténer hátsó falánál pedig
\(\displaystyle h_2=\frac{h}{2}+\frac{\ell}{2}\,\frac{a_0}{g}\)
értékre növekszik, a konténer közepénél pedig az álló helyzetnek megfelelő \(\displaystyle h/2\) marad (2. ábra).
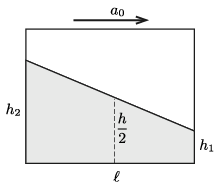
2. ábra
Jelöljük a tartály fenéklapjára ható erőt \(\displaystyle G\)-vel, a mozgásirányhoz viszonyított előlapnál ható erőt \(\displaystyle F_1\)-gyel, a hátsó oldallapra ható erőt \(\displaystyle F_2\)-vel, a trapéz alakú oldalfalra ható erőt pedig \(\displaystyle F_3\)-mal (3. ábra). Ezeket az erőket szeretnénk meghatározni.
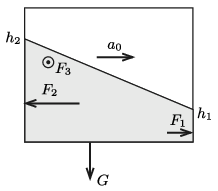
3. ábra
A folyadék által kifejtett nyomás mindenhol a légköri nyomáson felüli túlnyomást, vagyis a hidrosztatikai nyomást jelenti. (A légköri nyomás az alaplap és az oldallapok mindkét oldalánál hat, eredő erőt tehát nem hoz létre.)
A tartály fenéklapjára nyilván a folyadék súlyával megegyező nagyságú erő hat:
\(\displaystyle G=\frac{h}{2}\ell d \varrho g.\)
A folyadék hidrosztatikai nyomása a mélységgel arányosan növekszik. Az előlapra ható \(\displaystyle F_1\) erő a folyadék átlagos nyomása és a nyomott felület szorzataként kapható meg:
\(\displaystyle F_1=\left(\frac{1}{2}\varrho g h_1\right)\cdot \left(h_1d\right)=\frac{1}{8}\varrho g \,d \left(h-\ell\,\frac{a_0}{g}\right)^2.\)
Hasonlóan a hátsó lapra ható erő:
\(\displaystyle F_2=\left(\frac{1}{2}\varrho g h_2\right)\cdot \left(h_2d\right)=\frac{1}{8}\varrho g \,d \left(h+\ell\,\frac{a_0}{g}\right)^2.\)
Az oldalfal mentén a (túl)nyomás a folyadék (ferde) felszíne mentén nulla, függőlegesen lefelé haladva pedig a mélységgel arányosan lineárisan változik. Az átlagos nyomás egy-egy függőleges, a tartály előlapjától \(\displaystyle x\) \(\displaystyle (0\le x\le \ell)\) távol lévő, \(\displaystyle \Delta x\) széles,
\(\displaystyle h(x)=\frac{h}{2}+x\frac{a_0}{g} \)
magas sáv mentén:
\(\displaystyle \overline{p}=\frac12\varrho g h(x).\)
Ez az átlagos nyomás az egyes sávokra
\(\displaystyle \Delta F=\overline{p}\cdot h(x)\Delta x=\frac12\varrho g h^2(x)\Delta x,\)
a teljes oldalfalra pedig
\(\displaystyle F_3=\sum\frac12\varrho g h^2(x)\Delta x\)
erőt fejt ki.
Az összeget (vagyis az oldalfalra ható teljes nyomóerőt) pl. integrálszámítással, de elemi úton is meghatározhatjuk. Észrevehetjük, hogy ha az oldalfal folyadékkal érintkező részét egy \(\displaystyle \varrho\) felületi tömegsűrűségű (felületegységenként \(\displaystyle \varrho\) tömegű) vékony lemeznek képzeljük, és ezt a lemezt vízszintes helyzetben tartjuk, akkor a súlyerőnek a trapéz alapélére vonatkozó forgatónyomatéka éppen \(\displaystyle F_3\). No de ezt a forgatónyomatékot másképp is kiszámíthatjuk. Vágjuk szét (gondolatban) a trapézt egy \(\displaystyle \ell h_1\) területű téglalapra, valamint egy \(\displaystyle \ell\) és \(\displaystyle h_2-h_1\) befogójú derékszögű háromszögre. Ezen síkidomok súlypontjának és területének ismert képleteiből adódik, hogy
\(\displaystyle F_3=\varrho g\left[\ell h_1\cdot\frac{h_1}{2}+ \ell\frac{h_2-h_1}{2}\left(h_1+\frac{h_2-h_1}{3}\right)\right]= \varrho g \ell\frac{h_1^2+h_2^2+h_1h_2}{6}=\varrho g \ell\left(\frac{1}{8}h^2+\frac{1}{24} \ell^2 \frac{a_0^2}{g^2}\right) . \)
A megadott számértékekkel \(\displaystyle G=441~\rm kN\), \(\displaystyle F_1=14~\rm kN\), \(\displaystyle F_2=59~\rm kN\), \(\displaystyle F_3=114~\rm kN\).
Statistics:
37 students sent a solution. 5 points: Toronyi András. 4 points: Somlán Gellért. 3 points: 12 students. 2 points: 5 students. 1 point: 9 students. 0 point: 8 students.
Problems in Physics of KöMaL, September 2021
