 Problem P. 5345. (September 2021)
Problem P. 5345. (September 2021)
P. 5345. Two quarter circles of radius \(\displaystyle R\) are formed from two thin tubes and then two incomplete semi-circle shaped tubes are attached to them. The radius of the semicircles is \(\displaystyle r\) and the central angle of the missing part is \(\displaystyle \alpha\). Then the whole arrangement is attached to a vertical surface as shown in the figure. Then a small marble is dropped, at zero initial speed into the tube at point \(\displaystyle A\). The marble slides along the circular arcs of \(\displaystyle AB\) and \(\displaystyle BC\), then it falls freely between points \(\displaystyle C\) and \(\displaystyle D\) (oblique projectile motion). Then the marble slides along the circular arcs of \(\displaystyle DB\) and \(\displaystyle BE\). (Friction and air drag can be neglected everywhere.)
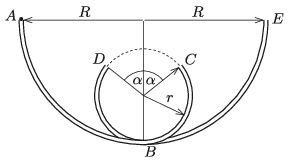
\(\displaystyle a)\) What is the measure of the angle \(\displaystyle \alpha\), if \(\displaystyle \frac{R}{r}=\frac{5}{2}\)?
\(\displaystyle b)\) Investigate at different \(\displaystyle \frac{R}{r}\) ratios at which value (or values) of \(\displaystyle \alpha\) is it possible for the marble to execute the above described motion.
(6 pont)
Deadline expired on October 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az energiamegmaradás tétele szerint a golyó sebessége a \(\displaystyle C\) pontban
\(\displaystyle v=\sqrt{2g(R-r-r\cos\alpha)},\)
amelynek függőleges és vízszintes komponense
\(\displaystyle v_\text{felfelé}=v\sin\alpha,\quad v_\text{balra}=v\cos\alpha.\)
A golyó valamekkora \(\displaystyle t\) idő alatt eljut a \(\displaystyle D\) pontba, ahol a sebessége ugyancsak \(\displaystyle v\) lesz. Fennáll tehát, hogy
\(\displaystyle gt=2v_\text{felfelé},\)
illetve
\(\displaystyle v_\text{balra}t=2r\sin\alpha.\)
(Feltehetjük, hogy \(\displaystyle \alpha>0\), tehát tényleges ferde hajításról van szó.) Ezekből az összefüggésekből \(\displaystyle t\) és \(\displaystyle v\) kiküszölése után ezt kapjuk:
\(\displaystyle \cos^2\alpha-\left(\frac{R}{r}-1\right)\cos\alpha+\frac{1}{2}=0.\)
\(\displaystyle a)\) Amennyiben \(\displaystyle \frac{R}{r}=\frac{5}{2}\), a fenti másodfokú egyenletből kapjuk, hogy \(\displaystyle \cos\alpha=0{,}5 \), azaz \(\displaystyle \alpha= 60^\circ\).
\(\displaystyle b)\) Bevezetve a \(\displaystyle \lambda=R/r\) jelölést, az \(\displaystyle \alpha\) szöget meghatározó egyenlet:
\(\displaystyle \cos^2\alpha-(\lambda-1)\cos\alpha+\frac12=0,\)
tehát
\(\displaystyle \cos\alpha= \frac{\lambda-1\pm \sqrt{\lambda^2-2\lambda-1}}{2}.\)
A négyzetgyök alatt nem állhat negatív szám, vagyis \(\displaystyle \lambda =\frac{R}{r}\ge 1+\sqrt{2}\approx 2{,}41\). A legkisebb arányhoz \(\displaystyle \alpha=45^\circ\)-os szög tartozik.
A \(\displaystyle \cos\alpha\)-ra nézve másodfokú egyenletnek \(\displaystyle \lambda>1+\sqrt{2}\) esetén két valós gyöke van. Az egyik gyök mindig kisebb 1-nél, a nagyobb gyök azonban \(\displaystyle \lambda>\frac52\) esetén 1-nél nagyobb, tehát számunkra érdektelen.
Összefoglalva: Ha \(\displaystyle 1+\sqrt{2}<\frac{R}{r}<\frac{5}{2},\) akkor minden \(\displaystyle R/r\) arányszámhoz kétféle \(\displaystyle \alpha\) is tartozhat. \(\displaystyle \frac{R}{r}>\frac{5}{2}\), illetve \(\displaystyle \frac{R}{r}=1+\sqrt{2}\) esetén csak egyetlen \(\displaystyle \alpha\) szög mellett mehet végbe a mozgás, míg \(\displaystyle \frac{R}{r}<1+\sqrt{2}\) esetén nincs olyan \(\displaystyle \alpha\) szög, ami mellett a leírt mozgás megvalósulhatna.
Statistics:
53 students sent a solution. 6 points: Antalóczy Szabolcs, Bencz Benedek, Biebel Botond, Fey Dávid, Hauber Henrik, Hegedűs Máté Miklós, Katona Attila Zoltán, Kertész Balázs, Kovács Márton András, Molnár Kristóf, Molnár-Szabó Vilmos, Mozolai Bende Bruno, Papp Marcell Imre, Schmercz Blanka, Seprődi Barnabás Bendegúz, Somlán Gellért, Téglás Panna, Toronyi András, Varga Mária Krisztina. 5 points: Gábriel Tamás, Kürti Gergely, Veszprémi Rebeka Barbara. 4 points: 9 students. 3 points: 13 students. 2 points: 5 students. 1 point: 1 student. 0 point: 2 students.
Problems in Physics of KöMaL, September 2021
