Problem P. 5357. (November 2021)

P. 5357. A uniform-density rod is lying on a horizontal tabletop. The rod is slowly raised into the vertical position by a force which is exerted at one end of the rod always perpendicularly to the rod. What is the least value of the coefficient of static friction between the rod and the tabletop if the rod does not slip during the process?

(5 pont)

Deadline expired on December 15, 2021.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Jelöljük a rúd súlyát \(\displaystyle G\)-vel, hosszát \(\displaystyle \ell\)-lel, a felső végénél ható erőt \(\displaystyle F\)-fel, az alsó végénél ható nyomóerőt \(\displaystyle N\)-nel, és végül a súrlódási erőt \(\displaystyle S\)-sel (lásd az ábrát).

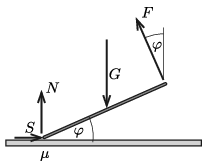
Amikor a rúd \(\displaystyle \varphi\) szöget zár be a vízszintessel, a következő összefüggések érvényesek:

\(\displaystyle S=F\sin\varphi\qquad \text{(vízszintes erők egyensúlya)},\)

\(\displaystyle N+F\cos\varphi=G\qquad \text{(függőleges erők egyensúlya)},\)

\(\displaystyle F\ell =G\frac{\ell}{2} \cos\varphi\qquad \text{(forgatónyomatékok egyensúlya)}.\)

Innen \(\displaystyle S\) és \(\displaystyle N\) kifejezhető \(\displaystyle G\) segítségével:

\(\displaystyle S=\frac{\sin\varphi\,\cos\varphi}{2}G,\)

\(\displaystyle N=\left(1-\frac{\cos^2\varphi}{2}\right) G.\)

A rúd akkor nem csúszik meg az alsó végpontjánál, ha

\(\displaystyle \mu>\frac{S}{N}=\frac{\sin\varphi\,\cos\varphi}{2-\cos^2\varphi}\equiv f(\varphi).\)

\(\displaystyle f(\varphi)\) arányos a \(\displaystyle 2\sin^2\varphi\) és a \(\displaystyle \cos^2\varphi\) mértani és számtani közepének a hányadosával, tehát akkor maximális, ha e két mennyiség megegyezik:

\(\displaystyle f(\varphi)= \frac{1}{\sqrt{8}}\cdot \frac{\sqrt{2\,\sin^2\varphi}\sqrt{\cos^2\varphi}} {\frac12\left(2\,\sin^2\varphi+\cos^2\varphi\right) }\le \frac{1}{\sqrt{8}}=\mu_\text{krit.}. \)

(Ugyanezt grafikus ábrázolással, vagy felsőbb matematikai módszerekkel is beláthatjuk.)

Ha tehát

\(\displaystyle \mu>\mu_\text{krit.}\approx 0{,}35,\)

akkor a rúd a felállítása során semelyik helyzeténél nem csúszik meg.

Statistics:

44 students sent a solution.
5 points:	Bányai Kristóf, Beke Bálint, Bencz Benedek, Czirók Tamás, Dóra Márton, Gábriel Tamás, Horváth 221 Zsóka, Kertész Balázs, Kovács Kristóf , Kürti Gergely, Magyar Gábor Balázs, Mészáros Ádám, Nagy 456 Imre, Nemeskéri Dániel, Pethő Dorottya, Schmercz Blanka, Somlán Gellért, Tárnok Ede , Téglás Panna, Toronyi András, Vágó Botond, Vig Zsófia.
4 points:	Csonka Illés, Fábián-Kovács Árpád, Waldhauser Miklós.
3 points:	5 students.
2 points:	2 students.
1 point:	2 students.
0 point:	6 students.
Unfair, not evaluated:	2 solutionss.

Problems in Physics of KöMaL, November 2021