 Problem P. 5360. (November 2021)
Problem P. 5360. (November 2021)
P. 5360. A simple Keplerian telescope is built for demonstration purposes. We have two converging lenses, one having a diameter of \(\displaystyle D\) and focal length \(\displaystyle f_1\), the other having a diameter of \(\displaystyle d\) and focal length \(\displaystyle f_2\) (\(\displaystyle f_1\gg f_2\), \(\displaystyle D>d\)), and we also have a shutter (a device that allows light to pass for a determined period) which can be fixed in the tube of the telescope at the common focal plane of the lenses. With the shutter we would like to control the direction of light rays forming the image.
\(\displaystyle a)\) What is the viewing angle of the telescope without the shutter? (That is: what is the maximum of the angular distance between two stars which can be seen in the telescope at the same time?)
\(\displaystyle b)\) At most what can the diameter of the shutter, which restricts the field of view of the telescope, be in order that the image should not get distorted (that is: the light rays determined by the directions of the rim of the image and pass the objective lens, also pass the eyepiece)?
\(\displaystyle c)\) Thus what can the field of view of the telescope be?
Hint: investigate how the parallel rays coming from different directions travel through the telescope.
(5 pont)
Deadline expired on December 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) Tekintsünk egy távoli csillagról érkező párhuzamos sugárnyalábot, ami az optikai tengellyel \(\displaystyle \alpha\) szöget zár be (1. ábra). (Az ábra az áttekinthetőség kedvéért erősen torzított, a valóságban \(\displaystyle \alpha\ll1\) radián.) A nyaláb az objektívtől \(\displaystyle f_1\) távol lévő fókuszsík \(\displaystyle F\) pontjában fókuszálódik, az optikai tengelytől \(\displaystyle f_1\alpha\) távolságban. (Kis szögekre \(\displaystyle \tg\alpha\approx \alpha\).)
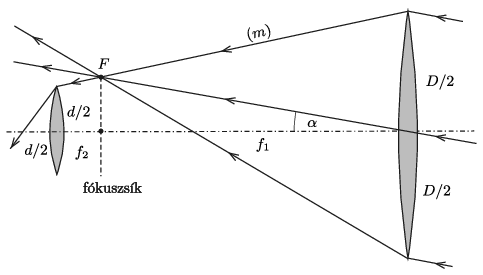
1. ábra
Egy csillag akkor esik bele a távcső látómezejébe, ha az objektív által megtört fénysugarak legalább egy része eléri a szemlencsét. Minél kevesebb ilyen fénysugár van, annál halványabb a csillag képe. A határesetnek az a helyzet felel meg, amikor az objektív tetejénél elhaladó \(\displaystyle (m)\) jelű fénysugár éppen eléri a szemlencse tetejét (1. ábra). Az \(\displaystyle (m)\) egyenes meredekségét kétféle módon is kiszámíthatjuk, és ezek nyilván egyenlőek:
\(\displaystyle \frac{D/2-f_1\alpha}{f_1}=\frac{(D/2)-(d/2)}{f_1+f_2},\)
ahonnan a távcső látómezejének nagysága (szögtávolságként kifejezve):
\(\displaystyle 2\alpha=\frac{1}{N+1}\left(\frac{d}{f_2}+\frac{D}{f_1}\right),\)
amit ilyen alakban is felírhatunk:
\(\displaystyle 2\alpha=\frac{(d+D/N)}{f_1+f_2}.\)
(\(\displaystyle N=f_1/f_2\) a távcső szögnagyítása.)
A látómező széle felé közeledve a szemlencsén egyre kevesebb fény jut át, a csillagok egyre halványabbnak látszanak, a távcső tehát fényerő tekintetében torzít.
\(\displaystyle b)\) Akkor nem lép fel fényerőtorzítás, ha az objektíven áthaladó összes fény bejut a szemlencsébe. Ez akkor valósul meg, ha a csillag iránya és az optikai tengely szöge nem nagyobb, mint a 2. ábrán látható \(\displaystyle \beta\) szög. A határesetnek az felel meg, amikor az objektív legaljánál elhaladó \(\displaystyle (n)\) jelű fénysugár éppen eléri a szemlencse tetejét.
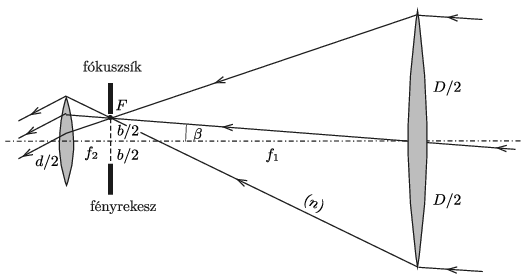
2. ábra
Az \(\displaystyle (n)\) egyenes meredekségét kétféle módon is kiszámíthatjuk, és ezek is nyilván egyenlőek:
\(\displaystyle \frac{D/2+f_1\beta}{f_1}=\frac{(D/2)+(d/2)}{f_1+f_2},\)
ahonnan a távcső torzításmentes látómezejének nagysága (szögtávolságként kifejezve):
\(\displaystyle 2\beta=\frac{1}{N+1}\left(\frac{d}{f_2}-\frac{D}{f_1}\right),\)
amit ilyen alakban is felírhatunk:
\(\displaystyle 2\beta=\frac{(d-D/N)}{f_1+f_2}.\)
Ha egy blendével csak a fényerőbeli torzítástól mentes fénysugarakat akarjuk átengedni, akkor ennek a fényrekesznek az átmérőjét
\(\displaystyle b=2f_1\beta=\frac{Nd-D}{N+1}\approx d-\frac{D}{N}\)
nagyságúra kell választanunk.
Megjegyzés. A feladatban \(\displaystyle D/N<d\) (tehát a fenti \(\displaystyle b\) és \(\displaystyle \beta\) pozitív), de elvben elképzelhető, hogy \(\displaystyle D/N>d\). Ekkor egy az objektíven áthaladó, eredetileg párhuzamos sugárnyaláb szélessége az okulár síkjában már nagyobb lesz, mint a szemlencse átmérője. Ebben az esetben a fényerő szerinti torzításmentesség feltétele az, hogy a szemlencse teljes terjedelmében essen bele az objektíven átjövő sugárnyalábba. A fentihez hasonló számolás alapján ez akkor teljesül a blende által megengedett minden irányra, ha
\(\displaystyle b=\frac{D-Nd}{N+1}\approx\frac{D}{N}-d,\)
és továbbra is \(\displaystyle \beta=\frac{b}{2f_1}\). Ilyen távcsövet azonban nem érdemes építeni, mert az objektív által felfogott fény egy része mindenképpen elvész, tehát a lehetségesnél kisebb lesz a kép fényessége.
Statistics:
3 students sent a solution. 4 points: Kertész Balázs. 2 points: 1 student. 1 point: 1 student.
Problems in Physics of KöMaL, November 2021
