 |
A P. 5363. feladat (2021. november) |
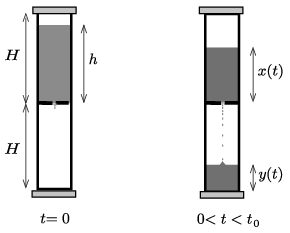
P. 5363. Egy vékony, magas üvegcsőből homokórát készítettünk. A benne lévő homok \(\displaystyle m_0\) tömege megegyezik az üvegcső és a tartótalpak együttes tömegével. Kezdetben a homok az alsó térfél \(\displaystyle h=5\) cm hosszú részét tölti ki, és az eszköz megfordítása után egyenletes ütemben \(\displaystyle t_0= 1\) perc alatt pereg le. (A felső és az alsó térfélben lévő homok alakját közelítsük hengerekkel.)

\(\displaystyle a)\) Határozzuk meg, hogy hol van a homokóra tömegközéppontja \(\displaystyle t\) idővel az óra elindítása után! (Ne foglalkozzunk a homokóra indítását követő, illetve a megállását közvetlenül megelőző nagyon rövid időtartamokkal, amikor a homokzuhatag még vagy már nem tölti ki a kifolyónyílás és az alsó becsapódási hely közötti teljes távolságot.)
\(\displaystyle b)\) Számítsuk ki, hogy mekkora a homokóra impulzusa (lendülete) \(\displaystyle t\) idővel a homokóra elindítása után!
\(\displaystyle c)\) Nagyon érzékeny mérleggel megmérjük a homokóra súlyát, miközben a homok a felső tartályból az alsóba pereg. Azt találjuk, hogy a mért súly egy kicsivel nagyobb, mint a már lepergett homokóra súlya. Az előző két részfeladatra adott választ felhasználva adjuk meg, hogy hány ezrelékkel nagyobb a működő homokóra súlya a már ,,lejárt'' homokóráénál!
Közli: Széchenyi Gábor, Budapest
(6 pont)
A beküldési határidő 2021. december 15-én LEJÁRT.
Megoldás. Az álló (már lepergett) homokóra súlya
\(\displaystyle G_0=\left(m_\text{homok}+m_\text{üvegcső}\right)g=2m_0g.\)
\(\displaystyle (i)\) A naiv (de hibás) érvelés szerint a működő homokóra súlya egy kicsit kisebb, mint az állóé, hiszen az éppen lefelé eső homok nem ér hozzá semmihez, tehát nem nyomja a mérleget. Ebben az érvelésben az a hibás, hogy nem veszi figyelembe a felgyorsult homokszemek által az alsó homokkupacnak átadott lendületet.
\(\displaystyle (ii)\) Kicsit árnyaltabb gondolatmenet szerint az egyenletesen lepergő homok miatt a berendezés tömegközéppontja egyenletesen süllyed lefelé, a tömegközéppont gyorsulása tehát nulla. Ennek megfelelően a nehézségi erő és a mérleg által kifejtett erő eredője nulla, tehát a mérleg \(\displaystyle 2m_0g\) súlyt mér. De még ez a megfontolás is hibás!
\(\displaystyle (iii)\) Ténylegesen a rendszer tömegközéppontja nem egyenletesen mozog, hanem egy kicsit gyorsul felfelé. A tömegközéppont szempontjából tekinthetjük úgy, hogy egységnyi idő alatt mindig ugyanannyi anyag kerül a felső térfélben lévő homok tetejéről a \(\displaystyle H\) távolsággal mélyebben elhelyezkedő alsó térfél homokkupacának tetejére. A két homokhenger teteje közötti távolság azonban időben változik: kezdetben \(\displaystyle H+h\), a lepergés végénél pedig csak \(\displaystyle H-h\), hiszen a felső részből fogy, az alsóban pedig növekszik a homokoszlop magassága. Emiatt ugyanannyi idő alatt kezdetben többet süllyed lefelé a rendszer tömegközéppontja, mint a folyamat végén, tehát a tömegközéppont felfelé gyorsul.
\(\displaystyle a)\) Jelöljük az óra megfordítása után \(\displaystyle t\) idővel kialakuló homokhenger magasságát a felső térfélben \(\displaystyle x(t)\)-vel, az alsóban pedig \(\displaystyle y(t)\)-vel. Az egyenletes homokpergés miatt felírhatjuk, hogy
\(\displaystyle x(t)=\left(1-\frac{t}{t_0}\right)h,\qquad \text{illetve}\qquad y(t)= \frac{t}{t_0} h.\)
Ezek ismeretében könnyen kiszámíthatjuk az egész rendszer (homok + üvegcső) tömegközéppontjának az óra talpához viszonyított magasságát:
\(\displaystyle X(t)=\frac{m_0\,(x(t)/h)\left(H+\frac{1}{2}x(t)\right)+m_0(y(t)/h)\,\frac12y(t)+m_0\,H }{2m_0} =\left(H+\frac{h}4\right)-\left(H+h\right)\frac{t}{2t_0}+ \frac{h}{2t_0^2}\,t^2.\)
Ez az időnek másodfokú függvénye, tehát egyenletesen gyorsuló mozgást ír le. Leolvashatjuk, hogy a tömegközéppont gyorsulása (felfelé):
\(\displaystyle a_\text{tkp}=\frac{h}{t_0^2}=\frac{0{,}05\ \rm m}{(60\ \rm s)^2}=1{,}4\cdot10^{-5}\ \frac{\rm m}{\rm s^2}.\)
(A tömegközéppont helyének kiszámítása során nem vettük figyelembe az éppen lehulló homokot, mert annak tömege az üvegcsövet teljes keresztmetszetében kitöltő homok \(\displaystyle m_0\) tömegéhez viszonyítva elhanyagolhatóan kicsi.)
\(\displaystyle b)\) A rendszer impulzusa három részből tehető össze.
1. A felső térfélben lévő homok tömege \(\displaystyle m(t)=m_0\left(1-\frac{t}{t_0}\right)\), és lefelé \(\displaystyle v_0=h/t_0\) sebességgel mozog, így az impulzusa (ha a felfelé irányt tekintjük pozitívnak):
\(\displaystyle I_1=-m(t)\,v_0=-m_0\frac{h}{t_0}\left(1-\frac{t}{t_0}\right).\)
2. Az éppen lefelé hulló, \(\displaystyle u_0\) kezdősebességgel induló homok \(\displaystyle \tau\) idő alatt éri el az alsó homokhenger tetejét, vagyis a megtett útja
\(\displaystyle H-y(t)=H-h\left(\frac{t}{t_0}\right)=u_0\tau+\frac{g}{2}\tau^2.\)
A kis nyíláson kieső homokszemek kezdősebessége \(\displaystyle u_0\), végsebessége \(\displaystyle u_1=u_0+g\tau\), és mivel a sebesség időben egyenletesen nő, az átlagsebesség:
\(\displaystyle \overline{u}(t)=\frac{u_0+u_1}{2}=u_0+\frac{g}{2}\tau.\)
A lehulló homok tömege \(\displaystyle m'=m_0\tau/t_0\), vagyis a homokzuhatag teljes impulzusa:
\(\displaystyle I_2=-m'\overline{u}=-\frac{m_0}{t_0}\left(u_0\tau+\frac{g}{2}\tau^2\right)=-\frac{m_0}{t_0}\left(H-y(t)\right)= -\frac{m_0}{t_0}\left(H-h\frac{t}{t_0} \right).\)
3. A már lehullott homok az alsó térfélben áll, tehát az impulzusa: \(\displaystyle I_3=0.\)
A homokóra teljes impulzusa:
\(\displaystyle I(t)=I_1+I_2+I_3=-\frac{m_0}{t_0}(H+h)+2m_0\frac{h}{t_0^2}\,t=\text{állandó}+2m_0\frac{h}{t_0^2}\cdot t.\)
Megjegzés. Érdekes, hogy a tömegközéppont helyének (sebességének és gyorsulásának) kiszámításakor a lehulló homok tömegét elhanyagolhattuk, az impulzus számításánál viszont a homokzuhatag lényeges járulékot adott. Ennek az az oka, hogy a lehulló rész tömege kicsi ugyan, de az átlagsebessége sokkal nagyobb, mint a felső térfélben lassan mozgó homokhengeré.
Bár látszólag más járulékokat vesz figyelembe, az \(\displaystyle I(t)\) impulzust a tömegközéppont \(\displaystyle X(t)\) pozíciójából kiolvasható
\(\displaystyle v_{\rm tkp}=-\frac{H+h}{2t_0}+\frac{h}{t_0^2}t\)
pillanatnyi sebesség segítségével is megkaphatjuk. A két eredmény azonos: a lepergő homok pont úgy járul hozzá a tömegközéppont áthelyeződéséhez, hogy az megfeleljen az impulzusának.
\(\displaystyle c)\) Az előző eredmények segítségével (akár a tömegközéppont gyorsulásából, akár a rendszer impulzusának időegységre eső változásából) kiszámíthatjuk a mérleg által mutatott erő nagyságát. A mérleg tányérja által kifejtett, felfelé irányuló \(\displaystyle +G\) erő és a \(\displaystyle -2m_0g\) nehézségi erő eredője idézi elő a \(\displaystyle 2m_0\) tömegű rendszer tömegközéppontjának \(\displaystyle a\) nagyságú gyorsulását, illetve a rendszer összimpulzusának változási sebességét:
\(\displaystyle G-G_0=2m_0a_\text{tkp} =2m_0\frac{h}{t_0^2}, \qquad\text{azaz}\quad G=G_0+2m_0\frac{h}{t_0^2}.\)
A relatív súlynövekedés:
\(\displaystyle \frac{\Delta G}{G_0}=\frac{G-G_0}{2m_0g}=\frac{h}{gt_0^2}=1{,}4\cdot10^{-6}=0{,}0014\ \text{ezrelék}.\)
Ugyanezt az eredményt kapjuk a kiszámított impulzusra vonatkozó Newton-egyenletből:
\(\displaystyle G-G_0=\frac{\Delta I(t)}{\Delta t},\)
ahonnan
\(\displaystyle \frac{\Delta G}{G_0}= \frac{h}{gt_0^2}=0{,}0014\ \text{ezrelék}.\)
Megjegyzés. Ez a jelenség egy hagyományos konyhai homokóra esetében csak precíziós mérleg használatával mutatható ki. Ellenben egy jól összeállított és méretezett kísérlet esetén az effektus akár otthoni vagy iskolai felszerelésekkel is mérhetővé válik. Ahhoz, hogy minél nagyobb \(\displaystyle \Delta G\)-t kapjunk, célszerű minél rövidebb lefolyású, kis keresztmetszetű, de nagy magasságú ,,homokórát'' készíteni, melyet nagy sűrűségű granuláris anyaggal töltünk ki. Jó választás lehet PET palackból kialakítani a ,,homokóra'' vázát, melyet vasgranulátummal töltünk fel. Ilyen mérési elrendezés mellett a vasgranulátum néhány másodperc alatt kifolyik a palack száján, és közben 0,1 g pontosságú digitális érzékelőkkel (erőmérő cellákkal) detektálhatjuk a jelenséget.
Statisztika:
11 dolgozat érkezett. 6 pontot kapott: Budai Csanád, Gábriel Tamás, Kertész Balázs, Téglás Panna, Toronyi András. 5 pontot kapott: Bencz Benedek. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 2 versenyző.
A KöMaL 2021. novemberi fizika feladatai

