 Problem P. 5364. (December 2021)
Problem P. 5364. (December 2021)
P. 5364. A solid half cylinder of radius \(\displaystyle R\), and of mass \(\displaystyle m\) is lying at rest on a flat, horizontal, frictionless surface with its curved surface facing upwards. From the top of the half cylinder a small object of mass also \(\displaystyle m\), starts from rest and slides down frictionlessly. How much distance does this small object cover sliding on the surface of the cylinder until it leaves it?
(5 pont)
Deadline expired on January 17, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jellemezzük a kis testnek a félhengeren elfoglalt helyzetét a függőlegessel bezárt \(\displaystyle \varphi\) szöggel, a félhengerhez viszonyított relatív sebességét az \(\displaystyle \omega=\frac{\Delta \varphi}{\Delta t}\) szögsebességgel, a félhenger pillanatnyi sebességét pedig jelöljük \(\displaystyle v\)-vel (lásd az ábrát).
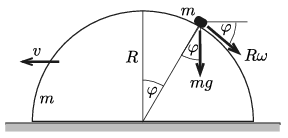
A laborrendszerben a kis test sebességének vízszintes komponense \(\displaystyle u_1=v-R\omega\cos\varphi\), függőleges komponense \(\displaystyle u_2=R\omega\sin\varphi\), a sebességének nagysága pedig
| \(\displaystyle (1)\) | \(\displaystyle u=\sqrt{u_1^2+u_2^2}=\sqrt{v^2+R^2\omega^2-2vR\omega\cos\varphi}.\) |
A rendszerre vízszintes irányban nem hat külső erő, ezért a vízszintes irányú impulzusa mindvégig nulla marad:
\(\displaystyle mv+mu_1= mv+m(v-R\omega\cos\varphi)=0,\)
azaz
| \(\displaystyle (2)\) | \(\displaystyle v= \frac{1}{2} R\omega \cos\varphi.\) |
Alkalmazhatjuk még a mechanikai energiamegmaradás törvényét:
| \(\displaystyle (3)\) | \(\displaystyle mgR(1-\cos\varphi)=\frac{1}{2}mv^2+\frac{1}{2}mu^2.\) |
Abban a pillanatban, amikor a kis test elválik a félhengertől, a közöttük ható nyomóerő éppen nullára csökken. A félhengerre ekkor nem hat vízszintes irányú erő, a gyorsulása tehát nulla. A félhengerhez rögzített koordináta-rendszer ekkor inerciarendszer, benne a Newton-féle mozgásegyenlet az eredeti alakjában érvényes. A kis testre az elválás pillanatában csak az \(\displaystyle mg\) nehézségi erő hat, amelynek sugárirányú (radiális) komponense \(\displaystyle mg\cos\varphi\). A sugárirányú gyorsulás \(\displaystyle R\omega^2\), a mozgásegyenlet szerint tehát
| \(\displaystyle (4)\) | \(\displaystyle mg\cos\varphi=mR\omega^2.\) |
Az (1)-(4) egyenletekből \(\displaystyle v\), \(\displaystyle u\) és \(\displaystyle \omega\) kiküszöbölése után ezt kapjuk:
\(\displaystyle \cos^3\varphi-6\cos\varphi+4=0.\)
Ez az egyenlet az \(\displaystyle x\equiv\cos\varphi\) változóra nézve harmadfokú:
\(\displaystyle x^3-6x+4=0,\)
aminek az egyik (számunkra érdektelen) gyöke: \(\displaystyle x_1=2\).
\(\displaystyle x^3-6x+4=(x-2)(x^2+2x-2)=0.\)
A másik két gyök: \(\displaystyle x_{2,3}=-1\pm\sqrt{3}.\) A \(\displaystyle (0,1)\) intervallumba csak \(\displaystyle x_2=\sqrt{3}-1\approx 0{,}73\) esik, ennek megfelelő szög: \(\displaystyle \varphi=\arccos x_2\approx0{,}75\) radián.
A kis test tehát \(\displaystyle s=R\varphi\approx \frac{3}{4}R\) hosszúságú utat tesz meg a félhengeren. (Ez természetesen nem egyezik meg a síklap koordináta-rendszerében megtett úttal, ez utóbbi kiszámítása lényegesen bonyolultabb lenne.)
Statistics:
50 students sent a solution. 5 points: Antalóczy Szabolcs, Bencz Benedek, Biebel Botond, Csapó Tamás, Czirók Tamás, Dóra Márton, Gábriel Tamás, Molnár Kristóf, Mozolai Bende Bruno, Nagy 456 Imre, Nemeskéri Dániel, Schmercz Blanka, Somlán Gellért, Toronyi András, Veszprémi Rebeka Barbara, Vincze Farkas Csongor. 4 points: Kürti Gergely. 3 points: 17 students. 2 points: 2 students. 1 point: 1 student. 0 point: 7 students. Unfair, not evaluated: 5 solutionss.
Problems in Physics of KöMaL, December 2021
