 Problem P. 5372. (December 2021)
Problem P. 5372. (December 2021)
P. 5372. The natural angular frequency of a physical pendulum made of a rod (a rigid uniform-density rod pivoted at one end) is \(\displaystyle \omega\). In the steady state of the oscillation, what is the amplitude of the oscillation of the bottom end of the rod if the pivoted end of the pendulum is moved horizontally with a displacement, which varies with time according to the following formula: \(\displaystyle x(t) = A\cos {(2\omega t)}\)? Air resistance is small but not negligible and \(\displaystyle A\omega ^2\ll g\).
(6 pont)
Deadline expired on January 17, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A szabad lengések körfrekvenciájából kiszámíthatjuk, hogy a fizikai inga \(\displaystyle \ell\) hossza és az \(\displaystyle \omega\) körfrekvencia közötti kapcsolat
\(\displaystyle T=2\pi\sqrt{ \frac{\frac{1}{3}m\ell^2}{mg\frac{\ell}{2}}},\)
ahonnan
| \(\displaystyle (1)\) | \(\displaystyle \omega=\frac{2\pi}{T}=\sqrt{\frac{3g}{2\ell}},\qquad \text{vagyis}\qquad \ell=\frac{3g}{2\omega^2}.\) |
(A megadott \(\displaystyle A\omega^2\ll g\) feltétel szerint \(\displaystyle A\ll \ell\), vagyis az inga \(\displaystyle \varphi\) szögkitérése feltehetően nagyon kicsi marad, és így érvényes, hogy \(\displaystyle \sin\varphi\approx \varphi\), valamint \(\displaystyle \cos\varphi\approx 1\).)
Megjegyzés. Kezdetben, amikor a rúd felső végpontját mozgatni kezdjük, a rúd szögkitérése nagy, akár \(\displaystyle 90^\circ\)-os is lehet. Ez azonban a közegellenállás miatt (akármilyen kicsi is az) idővel lecsillapodik, tehát az állandósult állapotban már kicsivé válik.
Jelöljük az \(\displaystyle m\) tömegű rúdra annak felfüggesztési pontjában ható vízszintes erőt \(\displaystyle F(t)\)-vel, az inga tömegközéppontjának vízszintes irányú elmozdulását \(\displaystyle y(t)\)-vel, a tömegközéppont pillanatnyi gyorsulását pedig \(\displaystyle a_y(t)\)-vel. (A vízszintes koordináta kezdőpontjának válasszuk a felső végpont rezgésének középpontját.) Az inga szögkitérése
\(\displaystyle \varphi(t)= \frac{2}{\ell}(y-x),\)
a szöggyorsulása pedig
\(\displaystyle \beta(t)=\frac{2}{\ell}\left[a_y(t)+4A\omega^2\cos(2\omega t)\right].\)
(Az egyes mennyiségek irányítását az ábrán látható módon értelmezzük.)
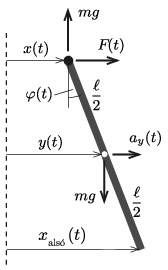
A rúdinga tömegközéppontjának függőleges irányú gyorsulása kis kitérések esetén – jó közelítéssel – nulla, így a felfüggesztési pontban függőlegesen felfelé ható erő \(\displaystyle mg\) nagyságú.
A rúd tömegközéppontjának (vízszintes irányú) mozgásegyenlete:
| \(\displaystyle (2)\) | \(\displaystyle F(t)=ma_y(t),\) |
a tömegközéppont körüli forgómozgásának egyenlete pedig
| \(\displaystyle (3)\) | \(\displaystyle -F(t) \frac{\ell}{2}-mg\left[y(t)-A\cos(2\omega t)\right]=\frac{1}{12}m\ell^2\cdot \frac{2}{\ell} \left[a_y(t)+4A\omega^2\cos(2\omega t)\right].\) |
Megjegyzés. A forgómozgás (3) egyenlete akkor is helyes, ha a tömegközéppont gyorsul. Más gyorsuló pontokra felírt hasonló egyenlet azonban hibás eredményre vezethet (lásd a ,,Merev testek mozgásegyenletei'' című cikket a honlapon, a fizika cikkek között az ,,Ami a tankönyvekből kimaradt, de a versenyzőknek hasznos lehet'' részben).
Az (1), (2) és (3) egyenletekből (\(\displaystyle \ell\) és \(\displaystyle F(t)\) kiküszöbölése után) kapjuk, hogy
\(\displaystyle a_y(t)+\omega^2y(t)=0. \)
Ez egy \(\displaystyle \omega\) körfrekvenciájú harmonikus rezgőmozgás egyenlete, amelynek megoldása
\(\displaystyle y(t)=K \cos\omega(t-t_0).\)
A \(\displaystyle K\) és a \(\displaystyle t_0\) állandókat a rúd középpontjának kezdeti helyzete és a kezdeti sebessége határozza meg.
A \(\displaystyle K\) amplitúdó – ha még a gyenge csillapítást is figyelembe vesszük – fokozatosan csökken, és elegendően hosszú idő múlva (vagyis az állandósult állapotban) nullává válik. Ebből az is következik, hogy az állandósult állapotban \(\displaystyle F(t)\equiv 0\). Mondhatjuk, hogy a kényszerrezgést végző rendszer – a csekély csillapítás miatt – fokozatosan ,,elfelejti'' a kezdőállapotát, és az állandósult állapotban a rezgés (lengés) menete a kezdeti adatoktól függetlenül mindig ugyanolyan lesz.
A rúd közepe tehát a rúdinga mozgása során – jó közelítéssel – mozdulatlan marad, és a felső végpontjának mozgatásához nincs szükség külső erőre. (Ez utóbbi állítás csak csillapításmentes esetben igaz. Ha a közegellenállás egy kicsi, de nem nulla csillapítást jelent, akkor a külső erő munkájának kell ellensúlyoznia a közegellenállásból adódó kicsiny energiaveszteséget.)
A rúd alsó végpontjának elmozdulása
\(\displaystyle x_\text{alsó}(t)=-x(t)=-A\cos(2\omega t).\)
A rúd alja tehát a felső végponttal azonos amlitúdójú, de azzal ellentétes fázisú, \(\displaystyle 2\omega\) körfrekvenciájú harmonikus rezgómozgást végez.
Statistics:
6 students sent a solution. 5 points: Gábriel Tamás. 4 points: 4 students.
Problems in Physics of KöMaL, December 2021
