Problem P. 5389. (February 2022)

P. 5389. A (point-like) fly flies at a constant speed of \(\displaystyle v\) parallel to the principal axis of a lens, having a focal length of \(\displaystyle f\), at a distance of \(\displaystyle d\) from it. What is the least speed of the fly with respect to its image?

(5 pont)

Deadline expired on March 16, 2022.

Sorry, the solution is available only in Hungarian. Google translation

I. megoldás. A légy képét a nevezetes sugármenetek segítségével kaphatjuk meg (1. ábra). A kép biztosan rajta van az optikai tengelytől \(\displaystyle d\) távolságban lévő \(\displaystyle AP\) egyenes megtört fénysugarán, vagyis az \(\displaystyle AF\) egyenesen, amely \(\displaystyle \alpha={\rm arctg}\, \frac{d}{f}\) szöget zár be az optikai tengellyel. A kép \(\displaystyle \boldsymbol u\) sebességgel mozog az \(\displaystyle AF\) egyenes mentén, nagysága attól függ, hogy a légy éppen hol tartózkodik. (\(\displaystyle u\) nulla és végtelen között bármilyen értéket felvehet.)

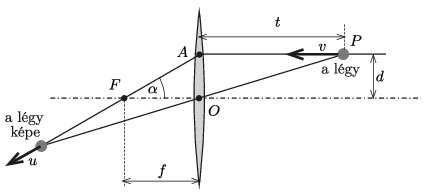
1. ábra

A légy és a légy képének \(\displaystyle \boldsymbol w\) relatív sebessége a 2. ábrán látható szerkesztéssel határozható meg. \(\displaystyle \boldsymbol w\) nagyságának legkisebb értéke annak a helyzetnek felel meg, amelynél \(\displaystyle \boldsymbol w\) merőleges \(\displaystyle \boldsymbol u\)-ra, és ilyenkor (lásd a 3. ábrát)

\(\displaystyle w_\text{min}=v\sin\alpha= v\frac{d}{\sqrt{d^2+f^2}}.\)

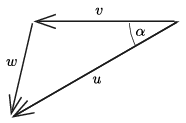
2. ábra

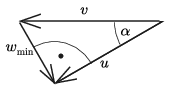
3. ábra

II. megoldás. Számítsuk ki a légy képének sebességét, annak az optikai tengellyel párhuzamos (\(\displaystyle u_1\)), illetve merőleges (\(\displaystyle u_2\)) komponensét. Célszerű lesz, ha a \(\displaystyle t\) tárgytávolság és a \(\displaystyle k\) képtávolság helyett az

\(\displaystyle x=t-f \qquad \text{és} \qquad y=k-f\)

változókat használjuk, ahogy ezt Newton is tette. A leképezési törvény ezekkel a változókkal így néz ki:

\(\displaystyle x\cdot y=f^2.\)

Az optikai tengellyel párhuzamos sebességkomponens

\(\displaystyle u_1=\frac{\Delta k}{\Delta t}=\frac{\Delta y}{\Delta t},\)

a \(\displaystyle t\) tárgytávolság változás sebessége pedig

\(\displaystyle \frac{\Delta x}{\Delta t}=-v.\)

Egy adott pillanatbeli és annál egy kicsiny \(\displaystyle \Delta t\) időtartammal későbbi állapot között fennáll, hogy

\(\displaystyle xy=f^2, \qquad \text{illetve}\qquad (x-v \Delta t)(y+\Delta y)=f^2,\)

ahonnan

\(\displaystyle u_1=\frac{\Delta y}{\Delta t}=v\frac{y}{x}+v\frac{\Delta y}{x}\approx v\frac{y}{x}=v\frac{f^2}{x^2}.\)

A légy képének és a légynek a relatív sebességét \(\displaystyle \boldsymbol w\)-vel jelölve, ennek a vektornak az optikai tengely irányú komponense:

\(\displaystyle w_1=u_1-v=v\left(\frac{f^2}{x^2}-1\right).\)

A légy képének az optikai tengelytől mért távolsága:

\(\displaystyle K=d\frac{k}{t}=\frac{ fd}{t-f}=\frac{fd}{x}.\)

A fentiekhez hasonló megfontolással adódik, hogy

\(\displaystyle w_2=u_2=\frac{\Delta K}{\Delta t}=v \frac{fd }{x^2}.\)

A relatív sebesség nagyságának négyzete:

\(\displaystyle \vert\boldsymbol w\vert^2=w_1^2+w_2^2=v^2\left(\frac{f^2}{x^2}-1\right)^2+v^2\frac{f^2d^2}{x^4},\)

ennek legkisebb értékét keressük.

Teljes négyzetté alakítással kapjuk, hogy

\(\displaystyle w^2=\left(\frac{vf\sqrt{f^2+d^2}}{x^2}-\frac{vf}{\sqrt{f^2+d^2}}\right)^2+ \frac{d^2v^2} {f^2+d^2} \ge v^2\frac{d^2} {f^2+d^2},\)

azaz

\(\displaystyle w\ge w_\text{min}=v\frac{d}{\sqrt{f^2+d^2}}.\)

Statistics:

13 students sent a solution.
5 points:	Antalóczy Szabolcs, Biebel Botond, Gábriel Tamás, Kertész Balázs, Téglás Panna.
4 points:	Mozolai Bende Bruno.
3 points:	1 student.
2 points:	5 students.
Unfair, not evaluated:	1 solutions.

Problems in Physics of KöMaL, February 2022