 Problem P. 5390. (February 2022)
Problem P. 5390. (February 2022)
P. 5390. There is a small electric dipole of dipole moment \(\displaystyle p\) at the centre of the thin-walled uncharged metal spherical shell of radius \(\displaystyle R\), shown in the figure. Determine the surface charge density at points \(\displaystyle A\) and \(\displaystyle B\), which are interior points of the shell. Determine the surface density of the charge on the outer surface of the shell as well.
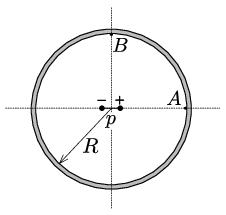
(Hint: Use the method of image charges applied for a sphere. It might be also useful to know the electric field due to a dipole at a point on the axial and equatorial lines.)
(6 pont)
Deadline expired on March 16, 2022.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Az elektromos dipólust két olyan, \(\displaystyle \pm q\) töltésű, pontszerű testnek gondolhatjuk, amelyek távolsága \(\displaystyle 2\epsilon\ll R\) és \(\displaystyle 2\epsilon q=p\). A dipólus elektromos tere a fémfelületen töltésátrendeződést indít el, ami mindaddig tart, amíg az eredő elektromos tér mindenhol merőleges nem lesz a fémfelületre.
A gömbi tükörtöltés módszere szerint az eredő elektromos tér a gömbhéj belsejében olyan, mintha a dipólus töltésein kívül még két másik elektromos töltés helyezkedne el a gömbhéjon kívül. Ezek töltése \(\displaystyle Q=\mp q\frac{R}{\epsilon}\), távolságuk pedig a gömbhéj középpontjától \(\displaystyle \frac{R^2}\epsilon\) (lásd az ábrát).
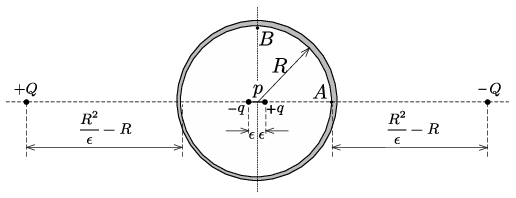
1. ábra
A fém gömbhéj falában nincs elektromos tér, és a gömbhéjon kívül is nulla a térerősség, hiszen a dipólus össztöltése nulla, és a gömbhéj is töltetlen. Így – a fluxustörvény szerint – a gömbhéj külső felületén az elektromos töltéssűrűség mindenhol nulla.
A gömbhéj belsejében az elektromos térerősséget a dipólus és a két tükörtöltés együttesen határozza meg. A felületi töltéssűrűség – a fluxustörvény szerint – a felületnél mérhető elektromos térerősség \(\displaystyle {\varepsilon_0}\)-szorosa.
A \(\displaystyle B\) pontban a \(\displaystyle \pm q\) és \(\displaystyle \mp Q\) töltéspár szimmetriája miatt az eredő térerősség sugár irányú komponense nulla, így a \(\displaystyle B\) pontban a felületi töltéssűrűség: \(\displaystyle \sigma_B=0\).
Számítsuk ki az eredő elektromos térerősséget az \(\displaystyle A\) pontban! (Kihasználjuk, hogy \(\displaystyle \epsilon\ll R\), hogy a gömbhéjba befelé mutató irányt tekintjük pozitívnak.)
\(\displaystyle E_A=\frac{q}{4\pi\varepsilon_0}\left( \frac{1}{(R-\epsilon)^2}-\frac{1}{(R+\epsilon)^2}\right)+ \frac{Q}{4\pi\varepsilon_0}\left(\frac{1}{\left( {R^2}/{\epsilon}+R\right)^2} +\frac{1}{\left( {R^2}/{\epsilon}-R\right)^2} \right)\approx \frac{1}{4\pi\varepsilon_0}\frac{6 \epsilon q}{R^3}=\frac{1}{4\pi\varepsilon_0}\frac{3p}{R^3}.\)
Innen következik, hogy a felületi töltéssűrűség az \(\displaystyle A\) pontban:
\(\displaystyle \sigma_A= -{\varepsilon_0}{E_A}=-\frac{3p}{4\pi R^3}.\)
II. megoldás. Ismerjük, vagy kézikönyvekben megtalálhatjuk, hogy az elektromos térerősség-vektor az ún. Gauss-féle főhelyzetekben, a dipólustól \(\displaystyle R\) távolságban:
\(\displaystyle {\boldsymbol E}_A^\text{(dipól)}=2\cdot\frac{1}{4\pi\varepsilon_0 R^3}{\boldsymbol p}=2{\boldsymbol E}_0,\)
illetve
\(\displaystyle {\boldsymbol E}_B^\text{(dipól)}=-\frac{1}{4\pi\varepsilon_0 R^3}{\boldsymbol p}=-{\boldsymbol E}_0.\)
A dipólus elektromos tere önmagában nem merőleges a fém gömbhéj felületére, ezért nem írja le helyesen a feladatban szereplő tényleges erőteret. De ha hozzáadunk a dipólus teréhez egy megfelelően választott homogén elektromos teret, akkor az eredő a gömbhéj belső felületénél mindenhol sugár irányú lesz, vagyis merőleges a fémfelületre.
Vajon milyen irányú és milyen nagyságú kell, hogy legyen ez a homogén erőtér? Az elrendezés szimmetriája miatt \(\displaystyle \boldsymbol p\)-vel párhuzamos (vagy azzal ellentétes irányú), a nagysága pedig éppen \(\displaystyle \vert {\boldsymbol E}_0\vert\), hiszen csak akkor teljesül, hogy a \(\displaystyle B\) pontban az eredő térerősségnek ne legyen érintőleges komponense. Ezek szerint
\(\displaystyle {\boldsymbol E}^\text{(összes)}={\boldsymbol E}^\text{(dipól)}+{\boldsymbol E}^\text{(homogén)}= {\boldsymbol E}^\text{(dipól)}-{\boldsymbol E}_B^\text{(dipól)}.\)
A kérdéses pontokban a térerősség nagysága:
\(\displaystyle E_A=2E_0-(-E_0)=3E_0=3p\cdot\frac{1}{4\pi\varepsilon_0 R^3},\)
illetve
\(\displaystyle E_B=-E_0-(-E_0)=0. \)
Ennek megfelelően a felületi töltéssűrűségek:
\(\displaystyle \sigma_A= -{\varepsilon}{E_A}=-3\frac{p}{4\pi R^3} \qquad \text{és} \qquad \sigma_B=0. \)
A gömbhéjon kívül az elektromos erőtér Coulomb-tér, aminek nagysága a gömbhéj belsejében lévő összes töltéssel arányos. Mivel ez a töltés nulla, kívül nincs elektromos erőtér, és így a felületi töltéssűrűség is nulla.
Megjegyzés. Megmutatjuk, hogy a dipól terének és a homogén elektromos térnek a szuperpoziciója valóban a fémfelületre merőleges vektorokat eredményez, nemcsak a Gauss-féle főhelyzetekben, hanem a dipól tengelyével tetszőleges \(\displaystyle \vartheta\) szöget bezáró helyvektorral jellemzett \(\displaystyle P\) pontban is.
A \(\displaystyle \boldsymbol p\) dipólmomentum vektor felbontható egy \(\displaystyle p\cos\varphi\) nagyságú \(\displaystyle \boldsymbol p_1\) és \(\displaystyle p\sin\varphi\) nagyságú \(\displaystyle \boldsymbol p_2\) vektor összegére (2. ábra). Ezen két dipólus szempontjából a \(\displaystyle P\) pont Gauss-féle (első, illetve második) főhelyzetnek számít, így a dipól terének komponensei:
\(\displaystyle E^\text{(dipól)}_\text{radiális}=2\cos\vartheta\,E_0,\)
\(\displaystyle E^\text{(dipól)}_\text{tangenciális}=-\sin\vartheta\,E_0,\)
ahol \(\displaystyle E_0\) az \(\displaystyle \frac{1}{4\pi\varepsilon_0}\frac{p}{R^3}\) mennyiséget jelöli.
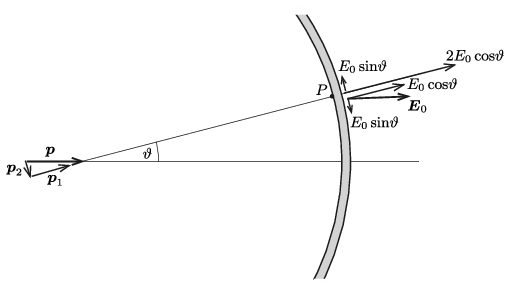
2. ábra
Szuperponáljuk a dipól terére az
\(\displaystyle \boldsymbol E_0=\frac{1}{4\pi\varepsilon_0 R^3}\boldsymbol p\)
térerősségvektorral megadott homogén elektromos mezőt. Ennek komponensei a gömbhéj belső felületénél:
\(\displaystyle E^\text{(homogén)}_\text{radiális}=\cos\vartheta\,E_0,\)
\(\displaystyle E^\text{(homogén)}_\text{tangenciális}=+\sin\vartheta\,E_0.\)
Az eredő térnek a gömbhéj felületénél a tangenciális komponense nulla, a radiális pedig:
\(\displaystyle E^\text{(eredő)}_\text{radiális}=3\cos\vartheta\,E_0=\frac{3p}{4\pi\varepsilon_0 R^3} \cos\vartheta.\)
Innen leolvasható, hogy a gömbhéj belső felületén a töltéssűrűség:
\(\displaystyle \sigma(\vartheta)=\frac{3p}{4\pi R^3}\cos\vartheta,\)
vagyis \(\displaystyle \vartheta=0\)-nál \(\displaystyle \sigma_A=\frac{3p}{4\pi R^3},\) valamint \(\displaystyle \vartheta=90^\circ\)-nál \(\displaystyle \sigma_B=0.\)
Statistics:
7 students sent a solution. 6 points: Schmercz Blanka. 5 points: Gábriel Tamás, Toronyi András. 4 points: 3 students. 2 points: 1 student.
Problems in Physics of KöMaL, February 2022
