 Problem P. 5399. (March 2022)
Problem P. 5399. (March 2022)
P. 5399. From a thin metal plate of width \(\displaystyle \delta\) a large conical surface was welded. A current of \(\displaystyle I\) flows from the vertex of the cone \(\displaystyle A\) to a point \(\displaystyle B\) which lies on a slant height of the cone. Determine both the magnitude and the direction of the current density vector at point \(\displaystyle C\) on the surface of the cone, if \(\displaystyle C\) opposite to \(\displaystyle B\). It is known that the distance of \(\displaystyle AB\) is equal to \(\displaystyle 3R\) and the distance between points \(\displaystyle B\) and \(\displaystyle C\) is \(\displaystyle 2R\).
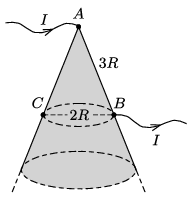
(6 pont)
Deadline expired on April 19, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az áramsűrűség olyan vektor, amely a töltések mozgásának irányába mutat, nagysága pedig a töltések mozgásirányára merőleges, egységnyi nagyságú felületen egységnyi idő alatt áthaladó töltések nagyságával egyezik meg.
Az egész elrendezés szimmetrikus az \(\displaystyle ABC\) síkra való tükrözésre, emiatt a \(\displaystyle C\) pontbeli áramsűrűség-vektor biztosan \(\displaystyle AC\) irányú. Ez annyit jelent, hogy az \(\displaystyle AC\) egyenesen keresztül sehol nem folyik áram, tehát a kúppalástot felvághatjuk az \(\displaystyle AC\) alkotója mentén, ettől nem változik meg az árameloszlás.
Terítsük ki síkba a felvágott fémlemezt! Mivel az \(\displaystyle AB\) távolság háromszor nagyobb, mint a \(\displaystyle CBC\) kör sugara, a kiterített fémlemez a teljes síknak egyharmada, \(\displaystyle 120^\circ\)-os szöget bezáró félegyenesek által határolt része lesz (1. ábra). Az ábrán a \(\displaystyle C\) pont két helyen is látható, a keresett áramsűrűség ezen két ponthoz tartozó áramsűrűségek összege.
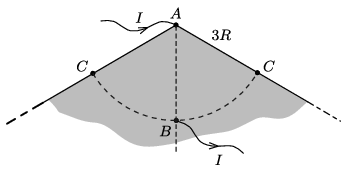
1. ábra
Ha egy teljes (,,végtelen nagy'') sík \(\displaystyle A\) pontjába \(\displaystyle I\) erősségű áramot vezetünk, az szimmetrikusan fut szét, és az áramsűrűség nagysága az áram bevezetési pontjától \(\displaystyle r\) távolságban lévő \(\displaystyle P\) pontban
\(\displaystyle j_A(P)=\frac{I}{2\pi\delta}\,\frac{1}{r},\)
iránya pedig \(\displaystyle AP\)-vel párhuzamos. Amennyiben a végtelen sík egy másik, \(\displaystyle B\) pontjánál \(\displaystyle I\) erősségű áramot vezetünk ki a fémből, az áramsűrűség nagysága a \(\displaystyle P\) pontban
\(\displaystyle j_B(P)=-\frac{I}{2\pi\delta}\,\frac{1}{r'},\)
ahol \(\displaystyle r'=BP\), iránya pedig \(\displaystyle BP\)-vel párhuzamos. Az eredő árameloszlás áramsűrűség-vektora \(\displaystyle \boldsymbol j_A\) és \(\displaystyle \boldsymbol j_B\) összege, szuperpoziciója.
A felvágott és kiterített kúppalást esetében a szuperpozició még nem adja meg a helyes árameloszlást, hiszen nem teljesíti azt a feltételt, hogy az \(\displaystyle AC\) félegyenes áramvonal legyen. Egy kis kiegészítéssel azonban mégis célhoz érhetünk, ha alkalmazzuk (az elektrosztatikai tükörtöltésekre emlékeztető) ,,tüköráram-módszerét''. Helyezzünk el – gondolatban – a ténylegesen létező fémsíkdarab mellé két másik \(\displaystyle 120^\circ\)-os csúcsszögű síkharmadot, és ezek mindegyikének csúcspontjánál vezessünk be \(\displaystyle I\) erősségű áramot (összesen tehát \(\displaystyle 3I\)-t), a \(\displaystyle B'\) és \(\displaystyle B''\) pontoknál pedig ugyanekkora erősségű áramot vezessünk el a síkból (2. ábra). Az ábrán a három tartomány között – az áttekinthetőség kedvéért – egy kicsiny távolságot hagytunk, de ezt a számolás során nulla szélességűnek kell tekintenünk.
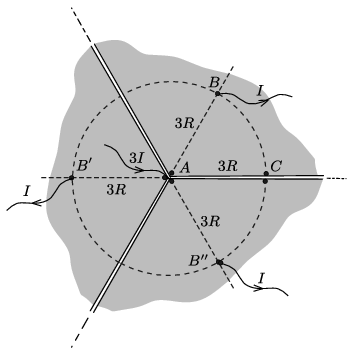
2. ábra
A síkharmad árameloszlását szuperponálva azt kapjuk, hogy a ténylegesen létező fémlemezben folyó árameloszlás olyan, mintha a végtelen sík \(\displaystyle A\) pontjába \(\displaystyle 3I\) erősségű áramot vezetnénk be, a \(\displaystyle B\), \(\displaystyle B'\) és \(\displaystyle B''\) pontoknál pedig \(\displaystyle I\)-t ki. Az elrendezés szimmetriája miatt a síkharmadokat határoló félegyenesek mindegyike áramvonal, tehát az eredeti fémlemezre vonatkozó határfeltétel valóban teljesül.
A \(\displaystyle C\) pontban az eredő áramsűrűség a 3. ábra szerint
\(\displaystyle \boldsymbol j(C)=\boldsymbol j_A(C)+\boldsymbol j_B(C)+\boldsymbol j_{B'}(C)+\boldsymbol j_{B''}(C),\)
ahol a vektorok nagysága:
\(\displaystyle j_A(C)=\frac{3I}{2\pi\delta}\,\frac{1}{3R},\qquad j_{B}(C)=j_{B''}(C)=\frac{I}{2\pi\delta}\,\frac{1}{3R} \qquad\text{és}\qquad j_{B'}(C)=\frac{I}{2\pi\delta}\,\frac{1}{6R}.\)
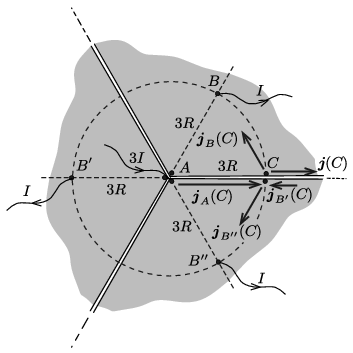
3. ábra
Az eredő áramsűrűség nagysága (az egyes összetevők irányát is figyelembe véve):
\(\displaystyle j(C)=j_A(C)-\frac{1}{2}j_{B}(C)-\frac{1}{2}j_{B''}(C)-j_{B'}(C)=\frac{I}{4\pi\delta R},\)
iránya pedig \(\displaystyle A\)-ból \(\displaystyle C\) felé mutat.
Statistics:
6 students sent a solution. 6 points: Gábriel Tamás, Toronyi András. 5 points: Téglás Panna. 3 points: 2 students. 2 points: 1 student.
Problems in Physics of KöMaL, March 2022
