 Problem P. 5417. (May 2022)
Problem P. 5417. (May 2022)
P. 5417. A small body of mass \(\displaystyle m\) is placed (but not fixed) onto the top of a thin cylindrical ring of radius \(\displaystyle R\) and of negligible mass being at rest on the horizontal ground. The system is displaced from its unstable equilibrium position. As the ring rolls faster and faster, the small body flies off somewhere.
\(\displaystyle a)\) What is the least value of the coefficient of static friction between the surfaces in contact if neither the small body on the ring nor the ring on the ground is skidding during the motion?
\(\displaystyle b)\) Where will the small object hit the ground?
(6 pont)
Deadline expired on June 15, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsük az abroncsnak azt a helyzetét, amelyben a kezdeti (labilis) egyensúlyi helyzetéhez képest csúszásmentesen gördülve \(\displaystyle \varphi\) szöggel elfordult, vagyis a \(\displaystyle C\) középpontja \(\displaystyle R\varphi\) utat tett meg. A kicsiny nehezék nem csúszik el az abroncson, nem is repül le róla, hanem egy ideig még az abroncs kezdetben legmagasabban lévő \(\displaystyle A\) pontjánál marad. Vegyük fel a kis testre, illetve az abroncsra ható erőket az 1. ábrán látható módon.
A kicsiny nehezékre \(\displaystyle mg\) nagyságú, függőlegesen lefelé mutató nehézségi erő hat, továbbá sugár irányban \(\displaystyle N\) nagyságú nyomóerővel és érintő irányban \(\displaystyle S\) nagyságú súrlódási erővel hat rá az abroncs.
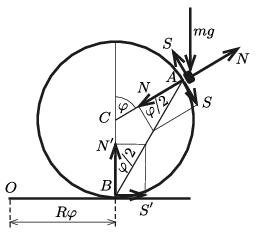
1. ábra
Az abroncsra az \(\displaystyle A\) pontban hat a nyomóerő és a súrlódási erő ellenereje, valamint a talajjal érintkező \(\displaystyle B\) pontjánál hat rá valamekkora \(\displaystyle N'\) nyomóerő és \(\displaystyle S'\) súrlódási erő. Ha a tapadó súrlódási együttható mindkét érintkező felületnél \(\displaystyle \mu_0\), akkor a csúszásmentes mozgás feltétele:
| \(\displaystyle (1)\) | \(\displaystyle \vert S \vert\le \mu_0N, \qquad \text{illetve}\qquad \vert S' \vert\le \mu_0N'.\) |
Ezeknek mindaddig fenn kell állni, ameddig a kis test le nem repül az abroncsról. Ez akkor következik be, amikor az \(\displaystyle N\) egészen nulláig csökken, majd előjelet váltva negatívvá ,,akarna'' válni. Az abroncs azonban nem tud húzóerőt kifejteni a kis testre, így az lerepül az abroncsról.
A továbblépéshez meg kell határoznunk az \(\displaystyle N(\varphi)\), \(\displaystyle S(\varphi)\), \(\displaystyle N'(\varphi)\) és \(\displaystyle S(\varphi)\) függvényeket. Ezt a Newton-féle mozgásegyenletek felírásával tehetjük meg.
Az abroncs tömege és a tehetetlenségi nyomatéka is elhanyagolhatóan kicsi, emiatt a rá ható erők eredőjének és a forgatónyomatékok eredőjének is nullának kell lennie. (Ezek a feltételek – jóllehet az abroncs gyorsul – megegyeznek a statikus egyensúly feltételeivel.) Az abroncs középpontjára vonatkoztatva csak a két súrlódási erőnek van forgatónyomatéka, és azok eredője akkor lesz nulla, ha
| \(\displaystyle (2)\) | \(\displaystyle S=S'.\) |
Azt is mondhatjuk, hogy az abroncsra az \(\displaystyle A\) pontban ható erők eredőjének hatásvonala át kell hogy menjen a \(\displaystyle B\) ponton (hogy arra vonatkoztatva ne legyen forgatónyomatéka), és hasonlóan a \(\displaystyle B\) pontban ható erők eredője \(\displaystyle A\) felé kell hogy mutasson. Az egyenlő szárú \(\displaystyle ABC\) háromszög egyik külső szöge \(\displaystyle \varphi\), és ez megegyezik a két (egyforma nagyságú) belső szög összegével. Így tehát fennáll
| \(\displaystyle (3)\) | \(\displaystyle \frac{S}{N}=\frac{S'}{N'}=\tg\frac{\varphi}{2}, \) |
és ebből (2) miatt
| \(\displaystyle (4)\) | \(\displaystyle N=N'.\) |
is következik. A tiszta gördülés és a kis test csúszásmentes mozgásának (1) feltétele szerint
| \(\displaystyle (5)\) | \(\displaystyle \mu_0\ge \tg\frac{\varphi}{2}.\) |
Ennek a feltételnek a kis test lerepülését jellemző \(\displaystyle \varphi_0\) szögig mindvégig fenn kell állnia, vagyis teljesülnie kell a
| \(\displaystyle (6)\) | \(\displaystyle \mu_0\ge \tg\frac{\varphi_0}{2}\) |
egyenlőtlenségnek.
Legyen az abroncs középpontjának sebessége és gyorsulása \(\displaystyle \varphi\) szögelfordulás után \(\displaystyle v(\varphi)\) és \(\displaystyle a(\varphi)\). A kis test sebessége két részből tevődik össze: a \(\displaystyle C\) pont \(\displaystyle v\) nagyságú vízszintes sebességéből és a körmozgás ugyancsak \(\displaystyle v\) nagyságú, de érintő irányú (a vízszintessel \(\displaystyle -\varphi\) szöget bezáró) kerületi sebességből (2. ábra).
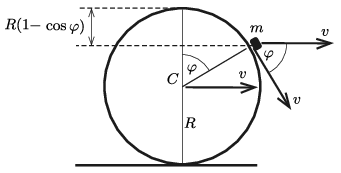
2. ábra
Az energiamegmaradás törvénye szerint
\(\displaystyle mgR(1-\cos\varphi)=\frac{m}{2}(v+v\cos\varphi)^2+\frac{m}{2}(-v\sin\varphi)^2=\frac{mv^2}{2}(2+2\cos\varphi),\)
tehát
| \(\displaystyle (7)\) | \(\displaystyle v^2=Rg\frac{1-\cos\varphi}{1+\cos\varphi}=Rg\,\tg^2\frac{\varphi}{2}.\) |
Mindaddig, amíg a kis test le nem repül az abroncsról, a két test egyetlen merev testnek tekinthető, amelynek az össztömege \(\displaystyle m\), tömegközéppontja a kis test \(\displaystyle A\) pontja, és a tömegközépppontjára vonatkoztatott tehetetlenségi nyomatéka elhanyagolhatóan kicsi, vagyis nullának tekinthető. Erre a merev testre csak három külső erő hat: \(\displaystyle \boldsymbol N'\), \(\displaystyle \boldsymbol S'\) és \(\displaystyle m\boldsymbol g\). A tömegközéppont gyorsulása három tagból áll: az abroncs \(\displaystyle C\) középpontjának vízszintes irányú és \(\displaystyle a\) nagyságú ,,transzlációs gyorsulásából'', a \(\displaystyle C\) pont körüli gyorsuló körmozgás ugyancsak \(\displaystyle a\) nagyságú, de érintő irányú kerületi gyorsulásából, és végül a körmozgás centripetális gyorsulásából, ami \(\displaystyle AC\) irányú és
\(\displaystyle a_{\rm cp}=\frac{v^2}{R}=g\,\tg^2\frac{\varphi}{2}\)
nagyságú (3. ábra).
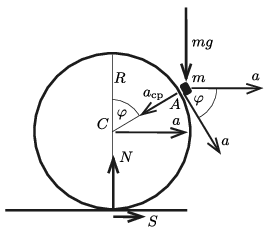
3. ábra
A Newton-egyenletek:
| \(\displaystyle (8)\) | \(\displaystyle N=m(g-g\,\tg^2\frac{\varphi}{2}\cos\varphi-a\sin\varphi) \qquad \text{(függőleges irányú mozgás egyenlete)},\) |
| \(\displaystyle (9)\) | \(\displaystyle S=m(a+a\cos\varphi-g\,\tg^2\frac{\varphi}{2}\sin\varphi) \qquad \text{(vízszintes irányú mozgás egyenlete)},\) |
| \(\displaystyle (10)\) | \(\displaystyle SR(1+\cos\varphi)-NR\sin\varphi=0 \qquad \text{(a forgás mozgásegyenlete)}.\) |
(Megjegyzés: A (10) egyenlet megegyezik a korábban már megkapott (3)-mal.)
A (8), (9) és (10) lineáris egyenletrendszer megoldása:
| \(\displaystyle (11)\) | \(\displaystyle N=mg\cos\varphi,\) |
| \(\displaystyle (12)\) | \(\displaystyle S=mg\frac{\sin\varphi \cos\varphi}{1+\cos\varphi},\) |
| \(\displaystyle (13)\) | \(\displaystyle a=\frac{\sin\varphi}{(1+\cos\varphi)}\,g.\) |
\(\displaystyle a)\) (11)-ből következik, hogy a kis test \(\displaystyle \varphi_0=\frac{\pi}{2}\) szögnél válik el az abroncstól, és ekkor vízszintes irányban is, és függőleges irányban is
\(\displaystyle v_0= \sqrt{Rg}\tg\frac{\pi}{4}=\sqrt{Rg}\)
sebessége van. A csúszásmentes mozgás feltétele az, hogy a tapadási súrlódási együttható legalább \(\displaystyle \mu_0^\text{min}=\tg\frac{\varphi_0}{2}=1\) legyen.
A további mozgás során a kis test \(\displaystyle R\) magasságból, \(\displaystyle v_0\) kezdősebességű szabadeséssel mozog. A talajra érkezés idejére
\(\displaystyle \frac{g}{2}t^2+v_0t=R\)
érvényes, ahonnan \(\displaystyle t_0=(\sqrt3-1)\frac{R}{g}\). Ennyi idő alatt a lerepülő test az abroncstól való elválás helyétől vízszintes irányban \(\displaystyle v_0t_0=(\sqrt3-1)R,\) az indulás \(\displaystyle O\) pontjától összesen
\(\displaystyle \frac{\pi}{2}R+R+(\sqrt3-1)R=\left(\frac{\pi}{2}+\sqrt3\right)R\approx 3{,}3\,R\)
távolságban éri el a talajt.
Megjegyzések. 1. Elvben elképzelhető lenne, hogy az abroncsról lerepülő kis test – még mielőtt elérné a talajt – összeütközik a \(\displaystyle v_0\) sebességgel guruló abronccsal. Ez azonban kizárt, hiszen a ferde hajítást elszenvedő kis test vízszintes irányú sebessége is \(\displaystyle v_0\), tehát mindvégig az abroncs szélével egyvonalban, az abroncs alatt található, tehát az \(\displaystyle O\) ponttól mért távolsága \(\displaystyle R\)-nél nagyobb.
2. A gördülő abronccsal együtt mozgó test pályája egy ciklois. A mozgás tehát éppen olyan, mint egy ciklois alakú, rögzített pályán súrlódásmentesen lecsúszó test mozgása. A test akkor repül le a cikloisról, amikor a kényszererő nullává válik, vagyis amikor a nehézségi erőnek a pályára merőleges komponense éppen megegyezik a centripetális gyorsulással. A ciklois jellemző adataiból (meredekség és görbület), valamint az energiamegmaradás törvényéből is megkapható a kényszerpálya elhagyásának helye.
3. A (13) összefüggést közvetlenül is megkaphatjuk, ha képezzük (7) mindkét oldalának az idő szerinti deriváltját:
\(\displaystyle \frac{{\rm d}}{{\rm d}t} \left(v^2\right)=2va= \frac{\rm d}{{\rm d}\varphi} \left( Rg\frac{1-\cos\varphi}{1+\cos\varphi}\right) \cdot \frac{{\rm d}\varphi}{{\rm d}t}=2Rg\frac{\sin\varphi}{(1+\cos\varphi)^2}\cdot \frac{v}{R}, \)
ahonnan
\(\displaystyle a=\frac{\sin\varphi}{(1+\cos\varphi)^2}\,g.\)
Ezt (8)-ba helyettesítve (11), (9)-be írva pedig (12) adódik.
4. Amikor a kis test lerepül az abroncsról, akkor \(\displaystyle N=S=0\). A kis test vízszintes irányú gyorsulása \(\displaystyle g-v_0^2/R=0\), függőleges irányú gyorsulása pedig \(\displaystyle a=g\). Érdekes, hogy az abroncs középpontjának vízszintes irányú gyorsulása közvetlenül a lerepülést megelőző pillanatban \(\displaystyle a=g\ne 0\), jóllehet az abroncsra ható erő ekkor nullává válik. Ez azonban nincs ellentmondásban Newton \(\displaystyle F=m_\text{abroncs}a\) törvényével, hiszen \(\displaystyle m_\text{abroncs}\) elhanyagolhatóan kicsi, nullának tekinthető.
Statistics:
4 students sent a solution. 3 points: 2 students. 2 points: 1 student. 1 point: 1 student.
Problems in Physics of KöMaL, May 2022
