 Problem P. 5453. (December 2022)
Problem P. 5453. (December 2022)
P. 5453. There is a point-like charge \(\displaystyle Q\) at a distance of \(\displaystyle d=0{.}5\) m from the centre of an uncharged metal sphere of radius \(\displaystyle r=0.2\) m. Determine the angle (with respect to the point charge) that is subtended by the points of the metal sphere with surface charge density equal to zero. (Numerical methods are also acceptable.)
(6 pont)
Deadline expired on January 16, 2023.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A felületi töltéssűrűség arányos a fémgömb felületénél kialakuló elektromos térerősség nagyságával, tehát a kérdés az, hogy ez a térerősség hol nulla.
A gömbön kívül kialakuló elektromos tér a gömbi tükörtöltés módszerével határozható meg. Az \(\displaystyle r\) sugarú gömb középpontjától \(\displaystyle d\) távolságban lévő \(\displaystyle Q\) töltés tükörtöltése egy, a gömb középpontjától \(\displaystyle \delta=kr\) távolságra elhelyezett \(\displaystyle -kQ\) töltés, ahol \(\displaystyle k=r/d<1\) állandó. A gömb felületén akkora lesz a térerősség, mint az ábrán látható módon elhelyezett \(\displaystyle Q\), \(\displaystyle -kQ\) és a gömb középpontjába helyezett \(\displaystyle +kQ\) töltés elektromos terének az eredője.
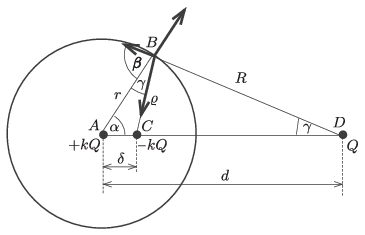
Az eredő térerősség mindenhol merőleges a gömb felületére, és a nagysága
| \(\displaystyle (1)\) | \(\displaystyle E=\frac{Q}{4\pi\varepsilon_0}\left(\frac{k}{r^2}-\frac{k\cos\gamma}{\varrho^2}-\frac{\cos\beta}{R^2}\right),\) |
ahol (a koszinusztétel szerint)
| \(\displaystyle (2)\) | \(\displaystyle \varrho=r\sqrt{1+k^2-2k\cos\alpha} \qquad \text{és}\qquad R=\frac{\varrho}{k}.\) |
(Kihasználtuk, hogy \(\displaystyle _\triangle ABC\) és \(\displaystyle _\triangle ADB\) hasonló háromszögek.)
Azt az \(\displaystyle \alpha\) szöget keressük, amelynél \(\displaystyle E=0\). A (2) összefüggéseket használva behelyettesíthetjük \(\displaystyle \varrho\)-t és \(\displaystyle R\)-t (1)-be, amely ezután így alakul:
| \(\displaystyle (3)\) | \(\displaystyle k\cos\beta+\cos\gamma=1+k^2-2k\cos\alpha.\) |
Két újabb koszinusztétel segítségével
| \(\displaystyle (4)\) | \(\displaystyle \cos\gamma=\frac{r^2+\varrho^2-\delta^2}{2r\varrho}=\frac{1-k\cos\alpha}{\sqrt{1+k^2-2k\cos\alpha}},\) |
illetve
\(\displaystyle \cos\beta=\frac{d^2-r^2-R^2}{2rR}=\frac{ \cos\alpha-k}{\sqrt{1+k^2-2k\cos\alpha}}.\)
Ezeket (3)-ba helyettesítve kapjuk, hogy
\(\displaystyle 1-k^2=\left(1+k^2-2k\cos\alpha\right)^{3/2},\)
vagyis
\(\displaystyle \cos\alpha=\frac {\left(1+k^2\right)-\left(1-k^2\right)^{2/3}} {2k}\)
adódik. Visszahelyettesítve (4)-be adódik a (tetszőleges \(\displaystyle k\)-ra érvényes) végeredmény:
\(\displaystyle \cos\gamma=\frac{(1-k^2)^{1/3}+(1-k^2)^{2/3}}{2}.\)
Esetünkben \(\displaystyle k=0{,}4\), ezért \(\displaystyle \cos\gamma=0{,}917\), azaz \(\displaystyle \gamma=23{,}51^\circ\). A kérdéses látószög tehát
\(\displaystyle 2\gamma=47{,}0^\circ.\)
Megjegyzés. Érdekes, hogy a kiszámított látószög nagyon jó közelítéssel megegyezik azzal a szöggel, amely alatt a teljes gömböt látjuk a \(\displaystyle Q\) töltés helyéről. Ez utóbbi
\(\displaystyle \gamma^*=\arcsin k=47{,}2^\circ.\)
Ez a közelítő egyezés nemcsak \(\displaystyle k=0{,}4\) esetén, hanem minden \(\displaystyle k\)-nál fennáll, tehát a zérus töltéssűrűségű hely majdnem a fémgömb látható részének legszélénél található. \(\displaystyle \gamma\) egy kicsit kisebb, mint \(\displaystyle \gamma^*\), de a relatív eltérésük tetszőleges \(\displaystyle k\) esetén kisebb, mint 2%.
Statistics:
7 students sent a solution. 6 points: Bencz Benedek, Halász Henrik, Schmercz Blanka. 3 points: 1 student. 2 points: 2 students.
Problems in Physics of KöMaL, December 2022
