 |
A P. 5470. feladat (2023. február) |
P. 5470. Két egyforma gyűjtőlencsét egymással szemben úgy helyezünk el, hogy fókuszpontjaik egybeesnek. Az egyik lencsét a közös optikai tengellyel párhuzamos, monokromatikus, egyenletes energiaáram-sűrűségű fénynyalábbal világítjuk meg. A lencsék antireflexiós (visszaverődést megakadályozó) réteggel vannak bevonva, a lencsék belsejében történő fényelnyelődéstől és az ottani visszaverődésektől eltekinthetünk.
\(\displaystyle a)\) Milyen irányú erő hat a lencsékre?
\(\displaystyle b)\) Becsüljük meg a lencsékre ható erők nagyságát!
Adatok: a lencsék fókusztávolsága 10 cm, átmérőjük 5 cm, a megvilágító nyaláb fényének hullámhossza 590 nm, az első lencsére 1 W fényteljesítmény jut.
Közli: Domokos Péter, Budapest
(5 pont)
A beküldési határidő 2023. március 16-án LEJÁRT.
Megoldás. \(\displaystyle a)\) Az idealizált feltételek miatt az első lencsére eső fotonok száma megegyezik az első lencsét elhagyó fotonok számával, sőt a második lencsére is ugyanennyi foton esik, és végül a második lencsét is ugyanennyi foton hagyja el. A lencsék tehát nem a fotonok számát változtatják meg, hanem a fotonok mozgásirányát (kivéve az optikai tengely mentén mozgó fotonokét). A fotonok \(\displaystyle p=h/\lambda\) impulzust hordoznak, ahol \(\displaystyle h\) a Planck-állandó, \(\displaystyle \lambda\) pedig a foton hullámhossza. Ha összeadjuk a fotonok egységnyi idő alatti impulzusváltozását, akkor megkapjuk a lencsére ható mechanikai erő nagyságát. Az első lencse csökkenti a beeső fotonok összimpulzusát, a második pedig növeli azt. Ennek megfelelően mindkét lencsére a fókuszpont felé mutató erő hat, amint ezt az alábbi ábra mutatja.
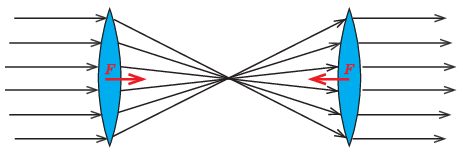
A két erő nagysága megegyezik, irányuk ellentétes, és ez emlékeztethet minket Newton harmadik törvényének erő-ellenerő párjára. Azonban nem a két lencse áll kölcsönhatásban egymással, hanem kétszeres fény-lencse kölcsönhatással van dolgunk. Ha például a második lencse átmérője kisebb lenne, akkor rá kisebb erő hatna, és így szóba sem kerülhetne a lencsék párkölcsönhatása.
\(\displaystyle b)\) A lencsék szélén történik a fotonok mozgásirányának legnagyobb megváltozása. A beeső fotonok maximális eltérülési szöge: \(\displaystyle \varphi=\arctg{\frac{d}{2f}}=14^{\circ}\), ahol \(\displaystyle d\) a lencsék átmérője, \(\displaystyle f\) pedig a fókusztávolságuk. Durva becslésként tekintsük úgy, hogy a fotonok átlagos eltérülése \(\displaystyle \frac{\varphi}2 = 7^{\circ}\). Egyetlen fotonnak az optikai tengellyel párhuzamos irányba eső ,,átlagos'' lendületváltozása:
\(\displaystyle \Delta p\approx p\left(1-\cos\frac{\varphi}2\right)=\frac{h}{\lambda}\left(1-\cos\frac{\varphi}2\right).\)
A \(\displaystyle \Delta t\) idő alatt beeső fotonok \(\displaystyle \Delta N\) számát a lencsékre jutó \(\displaystyle P\) fényteljesítményből határozhatjuk meg:
\(\displaystyle \Delta N=\frac{P\Delta t}{hc/\lambda},\)
ahol \(\displaystyle c\) a fénysebesség. Végül a lencsékre ható mechanikai erő nagyságát így számolhatjuk ki:
\(\displaystyle F=\frac{\Delta N\Delta p}{\Delta t}\approx\frac{P}{c}\left(1-\cos\frac{\varphi}2\right)=2{,}5\, \cdot \, 10^{-11}\,\rm{N}.\)
Megjegyzések. 1. Láthatjuk, hogy a lencsékre ható erők nagysága csak a megvilágítás teljesítményétől és a lencsék méretétől, valamint fókusztávolságától függ. A lencsékre eső fény hullámhossza kiesik a számításból, megadott értéke legfeljebb arra utal, hogy igazán jó antireflexiós réteget csak monokromatikus fényre lehet létrehozni.
2. Az \(\displaystyle F\) erő számszerű értékének becslését kicsit pontosabbá tehetjük a következő módon. Osszuk fel az \(\displaystyle R=2{,}5\) cm sugarú lencsére eső fotonokat két részre. Az egyik rész legyen az, amelynél a fotonok egy \(\displaystyle R/2\) sugarú körlapra esnek; az összes foton 1/4 része jut ide. A maradék rész egy \(\displaystyle R/2\) ,,széles'' körgyűrű, amelyre a fotonok 3/4 része esik. A körgyűrűre eső fény legnagyobb eltérülése \(\displaystyle 14^{\circ}\), a legkisebb pedig kb. \(\displaystyle 7^{\circ}\), átlaguk tehát \(\displaystyle 10{,}5^{\circ}\). A kis körlapnál a legnagyobb eltérülés \(\displaystyle 7^{\circ}\), a legkisebb nulla, az átlagukat vehetjük \(\displaystyle 3{,}5^{\circ}\)-nak. Ennek megfelelően a fotonok időegységre eső impulzusváltozása, vagyis az általuk kifejtett erő nagysága
\(\displaystyle F\approx \frac{P}{c}\left(\frac34(1-\cos 10{,}5^\circ)+ \frac14(1-\cos 3{,}5^\circ) \right)\approx 4{,}3 \, \cdot 10^{-11}\,\rm{N}.\)
3. Ha a lencse körlapját nagyon sok körgyűrűre osztjuk, és az ezekre eső fotonok járulékait összegezzük, akkor – határesetben (integrálszámítással) – megkapjuk az ,,egzakt''' eredményt. A lencsékre ható erők nagysága a legpontosabb számolás szerint \(\displaystyle F=5{,}06 \cdot 10^{-11}\,\rm{N},\) ami kicsit több, mint a kétszerese a durva becslésen alapuló számítás eredményének. Eszerint az átlagos szögeltérítés nem \(\displaystyle 7^{\circ}\), hanem majdnem \(\displaystyle 10^{\circ}\).
Statisztika:
7 dolgozat érkezett. 4 pontot kapott: Fajszi Karsa. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2023. februári fizika feladatai

