 Problem P. 5471. (February 2023)
Problem P. 5471. (February 2023)
P. 5471. Three identical cylinders of radius \(\displaystyle R\) and mass \(\displaystyle m\) are made from ice and they are all released without initial velocity from the position shown in the figure. The surface of the ice is smooth, so friction is negligible everywhere.
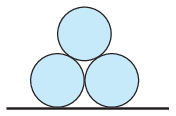
\(\displaystyle a)\) Determine and sketch the kinetic energy of one of the lower ice cylinders as a function of the displacement of the upper cylinder.
\(\displaystyle b)\) What is the speed at which the top ice cylinder hits the ground, and to what speed do the other two ice cylinders accelerate?
(6 pont)
Deadline expired on March 16, 2023.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsük azt a helyzetet, amikor az alsó két jéghenger tengelyének távolsága \(\displaystyle 2x\), a felső henger tengelye pedig \(\displaystyle R+y\) magasságban van (1. ábra). A jéghengerek sebessége \(\displaystyle \pm v_x\), illetve \(\displaystyle v_y\). Mivel a súrlódás elhanyagolható, a hengerek nem jönnek forgásba. Az indulás pillanatában
\(\displaystyle x=R;\qquad y=\sqrt3R\qquad\text{és}\qquad v_x=v_y=0.\)
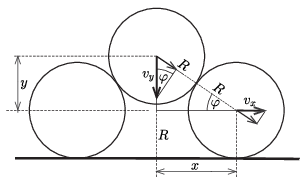
1. ábra
A középső henger (függőleges) elmozdulása így írható:
| \(\displaystyle (1)\) | \(\displaystyle s=\sqrt3R-y.\) |
A felső és bármelyik alsó jéghenger távolsága állandó, vagyis fennáll az
\(\displaystyle \sqrt{x^2+y^2}=2R\)
kényszerfeltétel. Ez a távolság akkor marad időben állandó, ha a sebességek megfelelő komponensei megegyeznek:
\(\displaystyle v_y\sin\varphi\left(\equiv v_y \dfrac{y}{2R}\right)=v_x\cos\varphi\left(\equiv v_x\frac{x}{2R}\right),\)
tehát
| \(\displaystyle (2)\) | \(\displaystyle v_y=v_x\dfrac{x}{y}=v_x\dfrac{\sqrt{4R^2-y^2}}{y}.\) |
Az energiamegmaradás tétele szerint
\(\displaystyle 2\cdot \frac12mv_x^2+\frac12mv_y^2=mgs,\)
vagyis (1) és (2) felhasználásával az alsó hengerek valamelyikének mozgási energiája
\(\displaystyle E=\frac12mv_x^2=mgR \frac{\sqrt3-(y/R)}{ 1+4(R/y)^2}.\)
Vezessük be a \(\displaystyle \xi=\frac{y}{R}\) és az \(\displaystyle {\cal E}= \dfrac{E}{mgR} \) dimenziótlan változókat (az \(\displaystyle s\) elmozdulás \(\displaystyle (\sqrt3-\xi)R\) alakban fejezhető ki). Fejezzük ki, majd ábrázoljuk \(\displaystyle \cal E\)-t \(\displaystyle \xi\), illetve \(\displaystyle s\) függvényében (2. ábra).
\(\displaystyle {\cal E}=\xi^2\frac{\sqrt3-\xi}{4+\xi^2}.\)
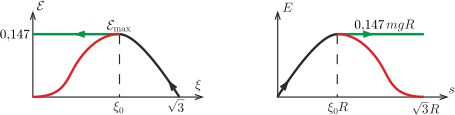
2. ábra
Az ábrán látszik, hogy csökkenő \(\displaystyle \xi\) (vagyis növekvő \(\displaystyle s\)) mellett \(\displaystyle \cal E\)-nek \(\displaystyle \xi=\xi_0=1{,}056\)-nál lokális maximuma van, ennél kisebb \(\displaystyle \xi\) értékeknél \(\displaystyle \cal E\) (és ezzel arányosan az \(\displaystyle E\) mozgási energia) egyre kisebbnek adódik, amint azt a grafikonok piros ága mutatja. Ha ez valóban így történne, akkor a felső jéghenger lassítaná az alsó hengereket, vagyis az érintkezési pontoknál nem tolná, hanem visszafelé húzná azokat. Ez nyilván nem lehetséges, hanem a hengerek elválnak egymástól, és a két alsó henger szabadon mozogva megtartja a mozgási energiáját (lásd a grafikonok zöld ágát), és \(\displaystyle v_\text{x,max}\) sebességgel fognak mozogni még akkor is, amikor a középső henger a talajhoz csapódik. Ez a sebesség
\(\displaystyle v_\text{x,max}=\sqrt{\dfrac{2E_\text{max}}{m}}= \sqrt{\dfrac{2mgR{\cal E}_\text{max}}{m}}=0{,}54\sqrt{Rg}.\)
A függőlegesen lefelé mozgó henger maximális mozgási energiáját ugyancsak az energiamegmaradás törvényéből kaphatjuk meg:
\(\displaystyle \frac12mv_\text{y,max}^2=\sqrt3 mgR-2E_\text{max}= (\sqrt3-2\cdot 0{,}147)mgR,\)
ahonnan
\(\displaystyle v_\text{y,max}=1{,}69\sqrt{Rg}.\)
Statistics:
13 students sent a solution. 6 points: Schmercz Blanka. 4 points: 1 student. 3 points: 1 student. 2 points: 5 students. 1 point: 3 students. 0 point: 1 student.
Problems in Physics of KöMaL, February 2023
