 Problem P. 5492. (May 2023)
Problem P. 5492. (May 2023)
P. 5492. Two identical bodies, each of mass \(\displaystyle m\), are connected by a flexible rubber thread, threaded through a stationary pulley of negligible mass. The bodies are held in the position shown in the figure – at this position the rubber band is unstretched – and then body \(\displaystyle B\) is released without initial velocity. Body \(\displaystyle A\) loses the contact with the table at time \(\displaystyle t_0\) after the release of body \(\displaystyle B\).
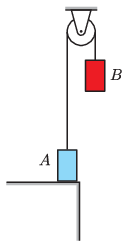
\(\displaystyle a)\) What is the displacement of body \(\displaystyle B\) at time \(\displaystyle t=t_0\)?
\(\displaystyle b)\) How long after the start will the velocity of body \(\displaystyle B\) be zero for the first time?
\(\displaystyle c)\) What is the maximum tension exerted in the rubber thread during the motion?
(5 pont)
Deadline expired on June 15, 2023.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Feltételezzük, hogy a gumiszál követi a Hooke-törvényt, vagyis a benne ébredő \(\displaystyle F\) erő arányos az \(\displaystyle x\) megnyúlással. Az arányossági tényezőt (a gumiszál ,,rugóállandóját'') jelöljük a szokásos módon \(\displaystyle D\)-vel.
\(\displaystyle a)\) A rendszer mozgása két szakaszra bontható. Az I. szakaszban az \(\displaystyle A\) test mozdulatlan, a \(\displaystyle B\) test pedig \(\displaystyle t_0\) ideig harmonikus rezgőmozgást végez. Ez a szakasz addig tart, amíg a gumiszálban ébredő erő kisebb, mint \(\displaystyle mg\), vagyis a \(\displaystyle B\) test elmozdulása
| \(\displaystyle (1)\) | \(\displaystyle x<\frac{mg}{D}=x_0.\) |
A \(\displaystyle B\) test sebessége kezdetben nulla, \(\displaystyle t_0\) idő elteltével pedig a gyorsulása válik nullává, mert ekkor a gumiszál által kifejtett erő éppen az \(\displaystyle mg\) nehézségi erő \(\displaystyle (-1)\)-szerese, tehát a testre ható eredő erő nulla (1. ábra).
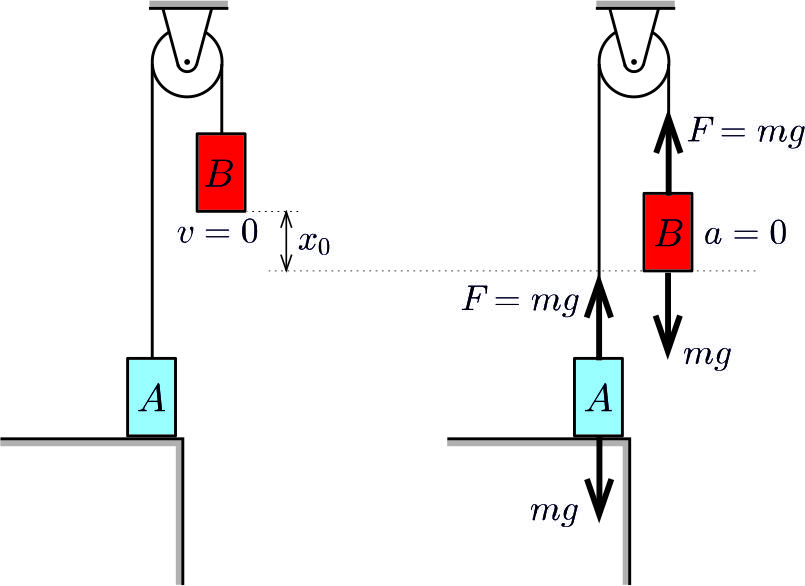
1. ábra
A harmonikus rezgőmozgás során a nulla sebességű és a nulla gyorsulású állapot között egy negyed periódusnyi idő telik el, vagyis
\(\displaystyle t_0=\frac{T}{4}=\frac{\pi}{2\omega}=\frac{\pi}{2}\sqrt{\frac{m}{D}},\)
és így
| \(\displaystyle (2)\) | \(\displaystyle \omega=\frac{\pi}{2t_0}\) |
Ezt (1)-gyel összevetve látjuk, hogy
| \(\displaystyle (3)\) | \(\displaystyle x_0=\frac{g}{\omega^2}=\frac4{\pi^2}gt_0^2,\) |
ekkora a \(\displaystyle B\) test elmozdulása a \(\displaystyle t_0\) idejű mozgás után.
A továbbiak szempontjából lényeges, hogy a \(\displaystyle B\) test sebessége a \(\displaystyle t_0\) idejű mozgás után
| \(\displaystyle (4)\) | \(\displaystyle v_0=x_0\omega=\frac{2}{\pi}gt_0.\) |
\(\displaystyle b)\) A mozgás második szakaszában mindkét test mozog. Tekintsük azt a helyzetet, amikor a \(\displaystyle B\) test elmozdulása \(\displaystyle x_0+x\), az \(\displaystyle A\) test az asztal fölött \(\displaystyle y\) magasságban van és az indulástól számítva \(\displaystyle t_0+t\), vagyis az \(\displaystyle A\) test megemelkedésének pillanatától mérve \(\displaystyle t\) idő telt el. A gumiszál megnyúlása ekkor \(\displaystyle x_0+x-y\), a szálat feszítő erő tehát
\(\displaystyle F=D(x_0+x-y).\)
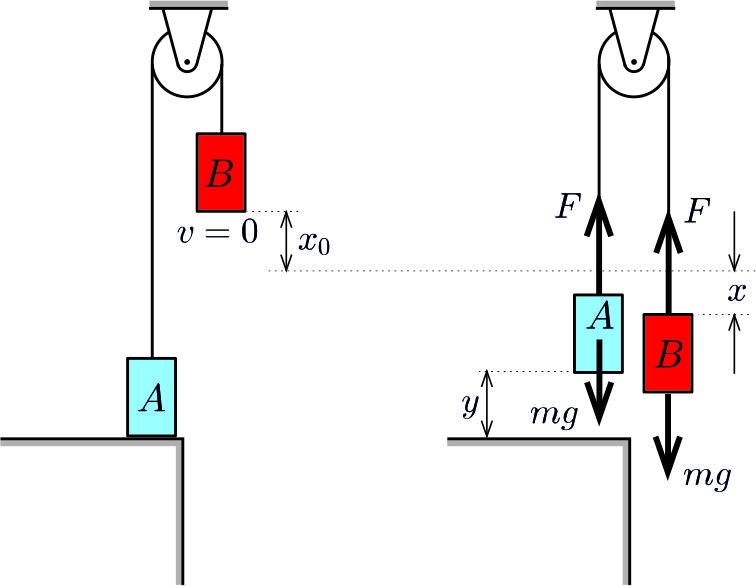
2. ábra
A testek mozgásegyenlete:
\(\displaystyle ma_x=mg-F=D(y-x), \qquad \text{illetve}\qquad ma_y=F-mg=D(x-y),\)
amiket így is felírhatunk:
| \(\displaystyle (5)\) | \(\displaystyle a_x=\omega^2(y-x)\) |
és
| \(\displaystyle (6)\) | \(\displaystyle a_y=\omega^2(x-y),\) |
és a kezdeti feltételek \(\displaystyle t=0\) pillanatban:
| \(\displaystyle (7)\) | \(\displaystyle x(0)=y(0)=0,\qquad v_x(0)=v_0, \qquad v_y(0)=0.\) |
(5) és (6) összegéből látszik, hogy az \(\displaystyle x(t)+y(t)\) mennyiség gyorsulása nulla, vagyis
| \(\displaystyle (8)\) | \(\displaystyle x(t)+y(t)=v_0\cdot t.\) |
Ez összhangban van a (7)-ben szereplő kezdeti feltételekkel.
(5) és (6) különbségét képezve:
\(\displaystyle a_{(x-y)}=-2\omega^2 (x-y),\)
ami egy \(\displaystyle \sqrt2\,\omega\) körfrekvenciájú harmonikus rezgőmozgás egyenlete. A kezdeti feltételeknek is eleget tevő megoldás:
| \(\displaystyle (9) \) | \(\displaystyle x(t)-y(t)=\frac{v_0}{\sqrt2\,\omega}\sin\left(\sqrt2\,\omega t\right).\) |
A \(\displaystyle B\) test mozgását leíró függvény (8) és (9) összegéből:
\(\displaystyle x(t)=\frac{v_0}{2}\left(t+\frac1{\sqrt2\,\omega}\sin (\sqrt2\,\omega t) \right),\)
és ennek megfelelően a \(\displaystyle B\) test sebessége:
\(\displaystyle v_x(t)=\frac{v_0}{2}\left(1+ \cos (\sqrt2\,\omega t) \right).\)
Ez a sebesség akkor válik nullává, amikor \(\displaystyle \sqrt2\,\omega t =\pi,\) vagyis
\(\displaystyle t=t_1=\frac{\pi}{\sqrt2\,\omega}=\sqrt2\,t_0.\)
Ennek megfelelően a \(\displaystyle B\) test sebessége az indulásától számítva
\(\displaystyle t_0+t_1=\left(1+\sqrt2\right)t_0\approx 2{,}41\,t_0\)
idő elteltével válik ismét nullává.
\(\displaystyle c)\) A gumiszálat feszítő erő akkor a legnagyobb, amikor az
\(\displaystyle x(t)-y(t)=\frac{v_0}{\sqrt2\,\omega}\sin\left(\sqrt2\,\omega t\right)\)
függvény maximális, nevezetesen
\(\displaystyle (x-y)_\text{max}=\frac{v_0}{\sqrt2\,\omega}=\frac1{\sqrt2}x_0\)
nagyságú. A gumiszálat feszítő erő ekkor
\(\displaystyle F_\text{max}=D\left(x_0+\frac1{\sqrt2}x_0\right)=\left(1+\frac1{\sqrt2}\right)mg\approx 1{,}71\ mg.\)
II. megoldás. Az állócsiga, mivel a tömege elhanyagolható, a gumiszálban ható erőnek csak az irányát változtatja meg, a nagyságát nem. Emiatt megtehetjük, hogy a gumiszálat (gondolatban) kiegyenesítjük, és a két test mozgását egy vízszintes, súrlódásmentes lapon vizsgáljuk. Az állócsigán lógó testekre ható nehézségi erőt ebben a ,,kiegyenesített'' elrendezésben egy-egy vízszintesen, \(\displaystyle mg\) nagyságú, ellentétes irányú külső erővel vehetjük figyelembe. Az eredeti asztal szerepét egy függőleges támaszték veszi át, amely egy ideig (amíg a gumiszálat feszítő erő kisebb, mint \(\displaystyle mg\)) megakadályozza az \(\displaystyle A\) test elmozdulását (3. ábra).

3. ábra
\(\displaystyle a)\) A mozgás kezdeti szakaszában az \(\displaystyle A\) test mozdulatlan, gyorsulása nulla. A gumiszálban ébredő \(\displaystyle F\) erő és az \(\displaystyle mg\) külső erő különbségét a függőleges támaszték által kifejtett \(\displaystyle K=mg-F\) nagyságú nyomóerő ,,egyensúlyozza ki''. Mivel \(\displaystyle K\ge0,\) ez a helyzet csak addig állhat fenn, amíg \(\displaystyle B\) test elmozdulása nem lépi túl a kritikus
\(\displaystyle x_0=\frac{mg}{D}\)
értéket. (Itt és a továbbiakban az I. megoldás jelöléseit használjuk.)
A \(\displaystyle B\) test eközben az elmozdulásával arányosan csökkenő gyorsulással, tehát \(\displaystyle \omega=\sqrt{D/m}\) körfrekvenciájú harmonikus rezgőmozgásnak megfelelő mozgást végez. A rezgőmozgás ,,egyensúlyi helyzete'' éppen az \(\displaystyle x_0\) elmozdulásnál lesz, itt válik a \(\displaystyle B\) test gyorsulása nullává. Kezdetben a \(\displaystyle B\) test sebessége nulla, tehát \(\displaystyle x_0\) elmozdulásáig éppen egy negyed periódus telik.
\(\displaystyle t_0=\frac14T=\frac14\cdot \frac{2\pi}{\omega},\)
vagyis
| \(\displaystyle (10)\) | \(\displaystyle \omega=\frac{\pi}{2t_0},\) |
és így
| \(\displaystyle (11)\) | \(\displaystyle x_0=\frac{mg}{D}=\frac{g}{\omega^2}=\frac{4gt_0^2}{\pi^2}.\) |
Az \(\displaystyle A\) test megmozdulásának pillanatában (4. ábra) a \(\displaystyle B\) test valamekkora \(\displaystyle v_0\) sebességgel rendelkezik. Ennek nagyságát a munkatétel alkalmazásával határozhatjuk meg:
\(\displaystyle mgx_0=\frac12Dx_0^2+\frac12mv_0^2,\)
ahonnan (10) és (11) felhasználásával:
| \(\displaystyle (12)\) | \(\displaystyle v_0=\sqrt{2gx_0-\omega^2x_0^2}=\frac{g}{\omega}=\frac2{\pi}gt_0.\) |
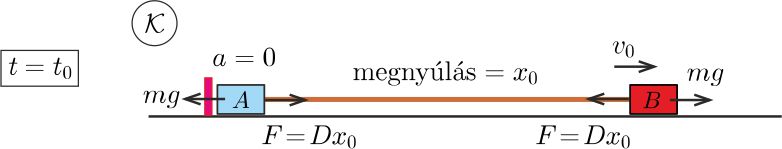
4. ábra
\(\displaystyle b)\) A mozgás további részében a külső erők (\(\displaystyle mg\) és \(\displaystyle -mg\)) eredője nulla, tehát a két testből álló rendszer lendülete időben állandó, a kezdeti \(\displaystyle mv_0\)-lal egyezik meg.
Térjünk át az asztal \(\displaystyle \cal K\) koordináta-rendszeréről a tömegközépponti, \(\displaystyle \cal K\)-hoz képest \(\displaystyle v_0/2\) sebességgel mozgó \(\displaystyle \cal K'\) vonatkoztatási rendszerre. Ebben a rendszerben a gumiszál \(\displaystyle S\) középpontja áll, az rögzítettnek is tekinthető.
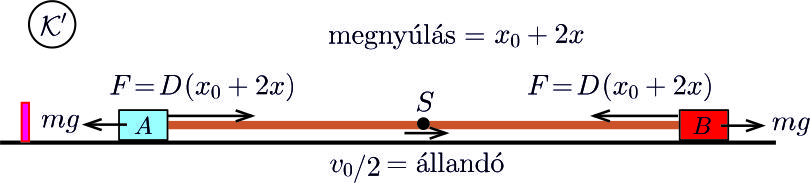
5. ábra
A fél gumiszál rugóállandója \(\displaystyle 2D\), hiszen adott feszítőerő hatására a gumi fele csak feleannyit nyúlik meg, mint a gumiszál egésze. A testek kezdősebessége a tömegközépponti rendszereben:
\(\displaystyle v'_A=0-\frac{v_0}{2}=-\frac{v_0}{2}, \qquad \text{illetve}\qquad v'_B=v_0-\frac{v_0}{2}=+\frac{v_0}{2}.\)
Amikor a fél gumiszál hossza \(\displaystyle \frac12x_0+x\), akkor a \(\displaystyle B\) testre ható erő:
\(\displaystyle F(x)=-2D\left(\frac12x_0+x\right)+mg=-2Dx,\)
a \(\displaystyle B\) test tehát
\(\displaystyle \omega'=\sqrt{\frac{2D}{m}}=\sqrt2\,\omega\)
körfrekvenciájú rezgésbe kezd.
Amikor a \(\displaystyle B\) test sebessége a \(\displaystyle \cal K\) rendszerben nulla, akkor a tömegközépponti \(\displaystyle \cal K'\) rendszerben a sebessége \(\displaystyle -v_0/2\), vagyis a kezdeti érték \(\displaystyle (-1)\)-szerese. Ezt a sebességet az \(\displaystyle A\) test megindulásától számítva éppen egy fél periódusnyi idő alatt éri el, ami
\(\displaystyle t_1=\frac{T'}{2}=\frac{\pi}{\omega'}=\frac{\pi}{\sqrt2\omega }=\sqrt2\,t_0.\)
A \(\displaystyle B\) test elindulásától számítva az első megállásáig tehát
\(\displaystyle t_0+t_1=\left(1+\sqrt{2}\right)t_0\)
idő telik el.
\(\displaystyle c)\) A gumiszálat feszítő erőt a gumiszál legnagyobb megnyúlása határozza meg. Ez legkönnyebben a \(\displaystyle \cal K'\) rendszerben kaphatjuk meg. Ha az egyes testek rezgési amplitúdója \(\displaystyle A\), akkor a legnagyobb megnyúlás \(\displaystyle x_0+2A\), és így
\(\displaystyle F_\text{max}=D\left(x_0+2A\right).\)
Az \(\displaystyle A\) amplitúdót a munkatételből határozhatjuk meg:
\(\displaystyle \cfrac{m}{2}\left(\frac{v_0}{2}\right)^2=\frac12(2D)A^2,\)
ahonnan
\(\displaystyle A=\sqrt{\cfrac{m}{8D}}v_0=\frac{1}{\sqrt8}x_0,\)
vagyis
\(\displaystyle F_\text{max}=\left(1+\frac{1}{\sqrt{2}} \right) mg.\)
Statistics:
13 students sent a solution. 5 points: Halász Henrik, Kis Márton Tamás. 3 points: 1 student. 2 points: 5 students. 1 point: 2 students. 0 point: 3 students.
Problems in Physics of KöMaL, May 2023
