 Problem P. 5507. (September 2023)
Problem P. 5507. (September 2023)
P. 5507. Two identical rough boards are attached to a horizontal fixed axle. Friction between the boards and the axle is negligible. Both boards have a mass \(\displaystyle m\) and a length \(\displaystyle \ell\).
A cylinder of mass \(\displaystyle M=\frac 12m\) and radius \(\displaystyle R=\frac 15\ell\) is placed between the boards.
\(\displaystyle a)\) What must the least value of the coefficient of static friction between the planks and the cylinder be so that the cylinder can remain in equilibrium somewhere (at a suitably chosen point)?
\(\displaystyle b)\) What can the angle subtended by the boards be when the cylinder is in equilibrium?

(6 pont)
Deadline expired on October 16, 2023.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen a deszkák által bezárt szög \(\displaystyle 2\varphi\), az egyes deszkák és a henger között ható nyomóerő \(\displaystyle N\), a súrlódási erő pedig \(\displaystyle S\) (lásd az 1. ábrát).

1. ábra
Mivel a deszkák és a henger érintkezési pontjai a forgástengelytől
\(\displaystyle OA=OA'=\frac{R}{\tg\varphi}=\frac{\ell}{5}\cdot \frac{\cos\varphi}{\sin\varphi}\)
távol vannak, továbbá \(\displaystyle OB=OB'=\ell/2\), a deszkáknak az \(\displaystyle O\) tengelyre vonatkoztatott forgatónyomaték-egyensúlyi feltétele:
\(\displaystyle N\,\frac{\ell}{5}\cdot \frac{\cos\varphi}{\sin\varphi}=mg\,\cfrac{\ell}{2}\sin\varphi,\)
vagyis
| \(\displaystyle (1)\) | \(\displaystyle N=\frac52 \,\frac{\sin^2\varphi}{\cos\varphi}\,mg.\) |
Teljesülnie kell még a hengerre ható erők egyensúlyi feltételének is. Az eredő erő vízszintes komponense a szimmetria miatt biztosan nulla, így elegendő a függőleges erőkomponenseket összegezni:
\(\displaystyle Mg+2N\sin\varphi-2S\cos\varphi=0,\)
ahonnan \(\displaystyle M=m/2\) és (1) felhasználásával
| \(\displaystyle (2)\) | \(\displaystyle S=\left( \frac{5\sin^3\varphi}{2\cos^2\varphi}+\frac{1}{4\cos\varphi} \right)mg \) |
adódik.
A tapadó súrlódás feltétele: \(\displaystyle S\le \mu N\), vagyis (1) és (2) ismeretében
\(\displaystyle \mu \ge \frac{S}{N}\equiv\tg\varphi+\frac{1}{10\,\tg^2\varphi}+\frac{1}{10}.\)
Ábrázolva az \(\displaystyle S/N\) hányadost \(\displaystyle \varphi\) függvényében a 2. ábrán látható görbét kapjuk.
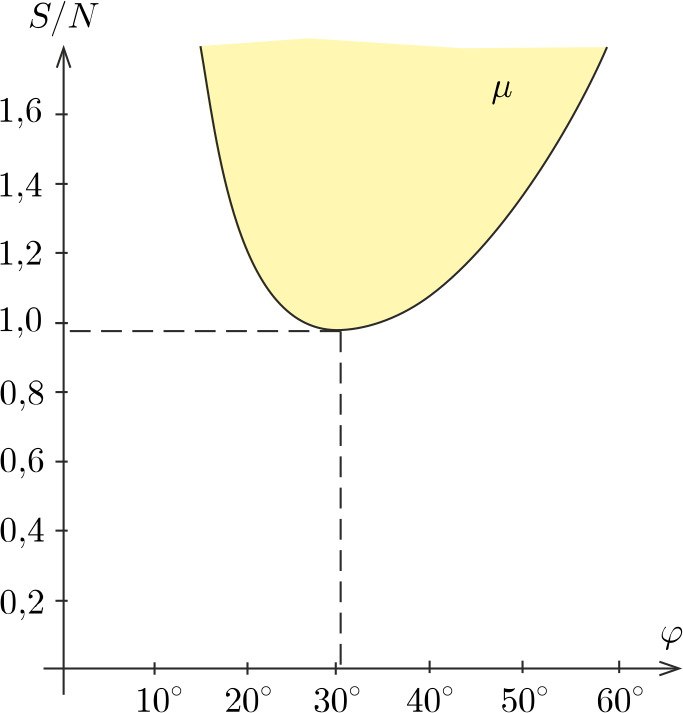
2. ábra
A tapadó súrlódás akkor tarthat egyensúlyt, ha \(\displaystyle \mu\) a sárga tartományba esik. Láthatjuk, hogy a
\(\displaystyle \mu\ge \mu_\text{min}\approx 1{,}0\)
feltételnek kell teljesülnie, és a legkisebb súrlódási együttható esetén csak a \(\displaystyle 2\varphi\approx 60^\circ\) szöget bezáró deszkák lehetnek egyensúlyban. Ha \(\displaystyle \mu\)-t valahogyan meg tudjuk növelni (pl. a deszkák felületét érdesebbé tesszük), akkor egyre szélesebb szögtartományban alakulhat ki egyensúly.
Ezeket az eredményeket más úton (grafikus ábrázolás vagy differenciálszámítás nélkül) is megkaphatjuk. Bevezetve az \(\displaystyle x\equiv\tg\varphi\) jelölést az egyensúly feltétele:
\(\displaystyle \mu \ge x+\frac{1}{10\,x^2}+\frac{1}{10}\equiv f(x).\)
Alkalmazva a számtani és mértani közepekre vonatkozó egyenlőtlenséget:
\(\displaystyle f(x)-\frac1{10}=\frac{x}{2}+\frac{x}{2}+\frac{1}{10\,x^2}\ge 3\sqrt[3]{\frac{x}{2}\cdot\frac{x}{2}\cdot\frac{1}{10\,x^2}}= \sqrt[3]{\frac{27}{40}}.\)
\(\displaystyle f(x)\) legkisebb értékénél fennáll:
\(\displaystyle \frac{x_0}{2}=\frac{1}{10\,x_0^2}, \qquad \text{vagyis}\qquad x_0=\frac{1}{\root 3 \of {5}}\qquad\text{és}\qquad \varphi_0=\arctg x_0=30{,}3^\circ.\)
A legkisebb súrlódási együttható:
\(\displaystyle \mu_\text{min}=f(x_0)=\sqrt[3]{\frac{27}{40}}+\frac1{10}=0{,}977\approx 1{,}0.\)
Megjegyzés. A deszkák és a henger érintkezési pontjai legfeljebb \(\displaystyle \ell\) távolságra lehetnek a tengelytől. Emiatt teljesülnie kell még a
\(\displaystyle \tg\varphi \ge \frac{R}{\ell}=\frac15,\qquad \text{vagyis}\qquad \varphi\ge 11{,}3^\circ\)
feltételnek is.
Statistics:
47 students sent a solution. 6 points: Alexandrova Angelina, Bencz Benedek, Csapó András, Csóka Péter, Daniils Koselevs, Debreceni Dániel, Fehérvári Donát, Hegedüs Márk, Hüvös Gergely, Képes Botond, Kiss 131 Adorján Timon, Kovács Kristóf , Lincoln Liu, Molnár Kristóf, Seprődi Barnabás Bendegúz, Szabó Donát, Tárnok Ede , Tóth Kolos Barnabás, Vidor Nikoletta, Vincze Farkas Csongor. 5 points: Beke Botond, Czirják Márton Pál, Diaconescu Tashi, Simon János Dániel, Žigo Boglárka. 4 points: 1 student. 3 points: 6 students. 2 points: 6 students. 1 point: 2 students. 0 point: 2 students. Not shown because of missing birth date or parental permission: 1 solutions.
Problems in Physics of KöMaL, September 2023
