 Problem P. 5514. (October 2023)
Problem P. 5514. (October 2023)
P. 5514. A point-like body with a charge \(\displaystyle -Q<0\) is fixed at point \(\displaystyle A\), which lies in a horizontal plane. In this plane, there is another point-like body of mass \(\displaystyle m\), and with charge \(\displaystyle q>0\) which can move without friction. Initially, the body of mass \(\displaystyle m\) is at point \(\displaystyle B\), and at this moment the initial distance of the charges is \(\displaystyle r_0\), and the body of mass \(\displaystyle m\) has a velocity of magnitude \(\displaystyle v_0=\sqrt{\frac{kqQ}{mr_0}}\), perpendicular to the line segment \(\displaystyle AB\) and parallel to the plane, as shown in the figure.
(The magnitude of the charges does not change during the motion.)
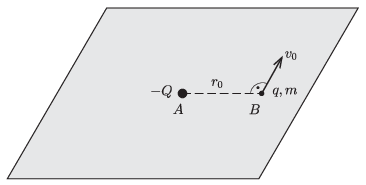
\(\displaystyle a)\) How much time elapses until the moving body returns to the line defined by the points \(\displaystyle AB\)?
\(\displaystyle b)\) Now the initial velocity of the moving body is halved. By what factor should the previously determined time be multiplied in order to get the time during which the moving body first reaches its furthest point from its initial position?
(5 pont)
Deadline expired on November 15, 2023.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Vízszintes síkon súrlódásmentesen mozog a \(\displaystyle q\) töltés, vagyis a földi súlyerővel a megoldás során nem kell törődnünk. Mivel a töltések közti elektrosztatikus vonzóerő helyfüggése megegyezik a gravitációéval, a mozgás leírására használhatjuk a Kepler-törvényeket: a mozgó töltés ellipszis- vagy körpályán fog keringeni a rögzített töltés körül (lásd az ábrát).
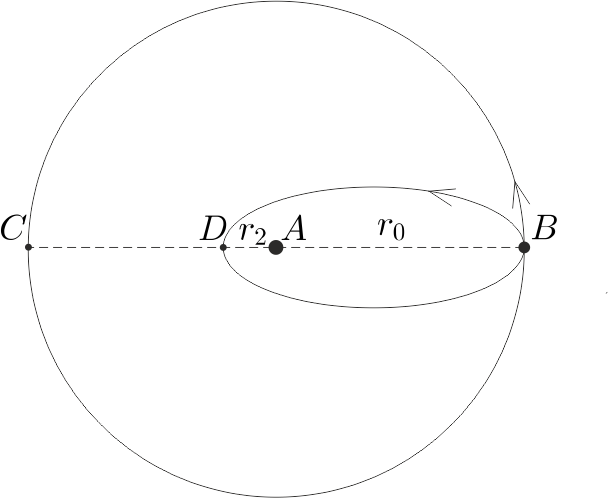
\(\displaystyle a)\) Amikor a töltött test \(\displaystyle v_0\) sebességgel \(\displaystyle r_0\) sugarú körpályán mozog, akkor:
\(\displaystyle \frac{mv_0^2}{r_0}=k\frac{qQ}{r_0^2},\qquad\textrm{ vagyis} \qquad v_0=\sqrt{\frac{kqQ}{mr_0}}.\)
A feladatban éppen ekkora, a testeket összekötő egyenesre (vezérsugárra) merőleges kezdeti sebességet adtak meg, tehát éppen a körpálya valósul meg. A pálya az \(\displaystyle AB\) egyenest egy félkörív megtétele után a \(\displaystyle C\) pontban \(\displaystyle t_a=\pi r_0/v_0\) idő múlva éri el.
\(\displaystyle b)\) Ettől kisebb kezdősebesség esetén a pálya ellipszis lesz. A pálya és az \(\displaystyle AB\) egyenes metszéspontjai (\(\displaystyle B\) és \(\displaystyle D\)) a pálya aphélium (naptávol) és perihélium (napközel) pontjai. A sebesség csak ebben a két pontban merőleges a vezérsugárra. Az első pontban a test távolsága és sebessége \(\displaystyle r_1=r_0\), \(\displaystyle v_1=\frac{1}{2}v_0\), a másodikban \(\displaystyle r_2\), \(\displaystyle v_2\). A kérdezett időarány a fél keringési idők aránya, amit Kepler III. törvényéből tudnánk kiszámolni, ha ismernénk az ellipszispálya nagytengelyének hosszát. Meg kell tehát határoznunk \(\displaystyle r_2\)-t.
Az ismeretlen \(\displaystyle r_2\) és \(\displaystyle v_2\) mennyiségekre két megmaradási törvényt tudunk felírni. A perdületmegmaradást:
\(\displaystyle m v_1 r_1=m v_2 r_2,\)
ami ebben az alakban csak \(\displaystyle B\)-ben és \(\displaystyle D\)-ben érvényes; valamint az energiamegmaradást:
\(\displaystyle \frac{1}{2}mv_1^2-\frac{kqQ}{r_1}=\frac{1}{2}mv_2^2-\frac{kqQ}{r_2},\)
ami a pálya mentén végig teljesül. Rendezzük át az utóbbi egyenletet, és használjuk a töltések és a tömeg helyett inkább a körpálya \(\displaystyle r_0\) és \(\displaystyle v_0\) paramétereit:
\(\displaystyle 2v_0^2 r_0 \bigg(\frac{1}{r_2}-\frac{1}{r_1}\bigg) = v_2^2 - v_1^2.\)
Helyettesítsük be a perdületmegmaradást kifejező \(\displaystyle \displaystyle v_2=\frac{v_1r_1}{r_2}\)-t:
\(\displaystyle 2v_0^2\frac{r_0}{r_1}\bigg(\frac{r_1}{r_2}-1\bigg) = v_1^2\Bigg(\bigg(\frac{r_1}{r_2}\bigg)^2 -1\Bigg).\)
Az egyenletnek könnyen megtalálható, de semmitmondó (triviális) gyöke az \(\displaystyle r_2=r_1\), ami magának a \(\displaystyle B\) pontnak a távolsága. Minket a másik \(\displaystyle r_2\ne r_1\) gyök érdekel, ezért eloszthatjuk az egyenletet \(\displaystyle \displaystyle \bigg(\frac{r_1}{r_2}-1\bigg)\)-gyel:
\(\displaystyle 2v_0^2\frac{r_0}{r_1} = v_1^2\bigg(\frac{r_1}{r_2}+1\bigg).\)
Helyettesítsük be a megadott \(\displaystyle r_1=r_0\) és \(\displaystyle v_1=\frac{1}{2}v_0\) kezdeti értékeket!
\(\displaystyle 2v_0^2 = \bigg(\frac{v_0}{2}\bigg)^2\bigg(\frac{r_1}{r_2}+1\bigg),\)
amiből az \(\displaystyle AD\) távolság: \(\displaystyle r_2=\frac{1}{7}r_0\). Az ellipszis és a körpálya nagytengelyeinek aránya tehát
\(\displaystyle \frac{1+\frac{1}{7}}{2} = \frac{4}{7},\)
a (fél) keringési időké pedig Kepler III. törvénye szerint
\(\displaystyle \bigg(\frac{4}{7}\bigg)^{3/2}\approx 0{,}43.\)
Statistics:
32 students sent a solution. 5 points: Bélteki Teó, Bencz Benedek, Csiszár András, Csóka Péter, Dobos Anita, Hüvös Gergely, Kis Márton Tamás, Kiss 131 Adorján Timon, Klement Tamás, Magyar Zsófia, Szabó Donát, Tárnok Ede . 4 points: Barna Márton, Csapó András, Fajszi Karsa, Masa Barnabás, Tóth Kolos Barnabás, Vágó Botond, Vincze Farkas Csongor. 3 points: 4 students. 2 points: 3 students. 1 point: 3 students.
Problems in Physics of KöMaL, October 2023
