Problem P. 5528. (December 2023)

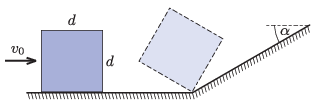
P. 5528. On a horizontal, frictionless surface, a cube of edge \(\displaystyle d=10~\textrm{cm}\) and of uniform mass distribution, is sliding at a velocity of \(\displaystyle v_0\). At some point the cube reaches a slope of an angle of inclination of \(\displaystyle \alpha=30^\circ\). The ``fault line'' between the slope and the ground is perpendicular to the direction of travel of the cube. The front edge of the cube which is in contact with the ground gets stuck at the fault line totally inelastically, so that the cube topples. What is the least value of \(\displaystyle v_0\) if the front face of the cube ``tips'' onto the slope?

(5 pont)

Deadline expired on January 15, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A megbillenő kocka az ütközés után a törésvonal, mint forgástengely körül valamekkora \(\displaystyle \omega\) szögsebességgel kezd el forogni. A lejtőre történő ,,ráborulás'' feltétele az, hogy \(\displaystyle 45^\circ\)-os szögelfordulása után a mozgási energiája pozitív (határesetben nulla) legyen.

A homogén tömegeloszlású kocka bármelyik élére vonatkoztatott tehetetlenségi nyomatéka \(\displaystyle \Theta=\frac23md^2\). (Ezt pl. a táblázatokban megtalálható tömegközéppontra vonatkoztatott tehetetlenségi nyomatékból a Steiner-tétel alkalmazásával kaphatjuk meg.)

Az ütközés utáni kezdeti szögsebességet a perdületmegmaradás tételének alkalmazásával határozhatjuk meg. A kocka kezdeti (a tömegközéppont mozgásából adódó) perdülete a törésvonalra vonatkoztatva \(\displaystyle mv_0d/2\), ütközés után pedig \(\displaystyle \Theta\omega\). Mivel az ütközés során fellépő erők hatásvonala a törésvonalon halad keresztül, ezek eredő forgatónyomatéka nulla, és így a perdület változatlan marad:

\(\displaystyle mv_0\frac{d}2=\frac23md^2\omega,\)

ahonnan

\(\displaystyle \omega=\frac34\frac{v_0}{d}.\)

A kocka mozgási energiája közvetlenül az ütközés után

\(\displaystyle E=\frac{1}{2}\Theta\omega^2=\frac{3}{16}mv_0^2.\)

Ennek az energiának kell fedeznie a gravitációs helyzeti energia növekedését az ,,éppen átbillenés'' határesetében:

\(\displaystyle \frac{3}{16}mv_0^2\ge mg\left(\frac{\sqrt2 d }{2}-\frac{d}{2}\right).\)

Innen az átbillenéshez szükséges sebesség:

\(\displaystyle v_0>\sqrt{\frac83\left(\sqrt2-1\right)gd}\approx 1{,}04\ \frac{\rm m}{\rm s}.\)

Statistics:

51 students sent a solution.
5 points:	Bogdán Benedek, Csapó András, Csiszár András, Czirják Márton Pál, Fekete Lúcia, Hegedüs Márk, Kis Márton Tamás, Kiss 131 Adorján Timon, Medgyesi Júlia, Molnár Kristóf, Molnár Zétény, Sipeki Árpád, Tárnok Ede .
4 points:	Seprődi Barnabás Bendegúz.
3 points:	3 students.
2 points:	10 students.
1 point:	16 students.
0 point:	3 students.

Problems in Physics of KöMaL, December 2023