 Problem P. 5534. (December 2023)
Problem P. 5534. (December 2023)
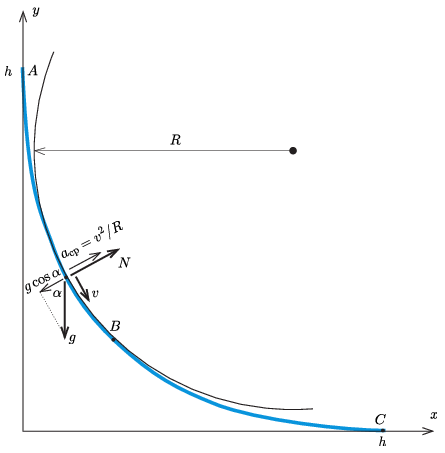
P. 5534. The \(\displaystyle x\)-axis of a Cartesian coordinate system is horizontal and the \(\displaystyle y\)-axis is vertical. Connect each point \(\displaystyle x=\xi\) of the \(\displaystyle x\) axis, \(\displaystyle 0\le \xi\le h=1~\mathrm{m}\), to the point \(\displaystyle y=h-\xi\) on the \(\displaystyle y\) axis. The yellow region in the figure shows the above defined line segments. Lay a frictionless, thin tube along the envelope of the line segments.
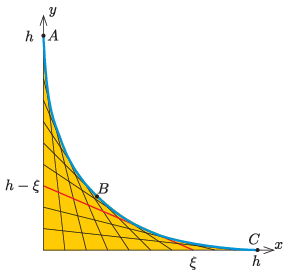
Launch a small body of mass \(\displaystyle m\) from the top of the tube without any initial speed. Determine the force in \(\displaystyle mg\) units with which the body pushes the wall of the tube during its motion
\(\displaystyle a)\) right after its start at point \(\displaystyle A\);
\(\displaystyle b)\) at point \(\displaystyle B\), which is the midpoint of the tube;
\(\displaystyle c)\) at point \(\displaystyle C\), which is a point right before the body leaves the tube.
(6 pont)
Deadline expired on January 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A megoldáshoz a következő lépések vezetnek el:
– Meghatározzuk a burkológörbe alakját;
– kiszámítjuk a kis test sebességét a kérdéses pontokban;
– meghatározzuk a cső görbületi sugarát a szóban forgó pontokban;
– és végül felírjuk a test Newton-féle mozgásegyenletét a burkológörbe érintőjére merőleges irányba, amiből megkapjuk a kérdezett nyomóerőt.
1. A burkológörbe meghatározása.
A \(\displaystyle \xi\) paraméterhez tartozó egyenes egyenlete:
| \(\displaystyle (1)\) | \(\displaystyle \frac{x}{\xi}+\frac{y}{h-\xi}=1.\) |
Tekintsünk egy adott \(\displaystyle (x,y)\) koordinátákkal rendelkező \(\displaystyle P\) pontot, és számítsuk ki, hogy mekkora \(\displaystyle \xi\) érték(ek)hez tartozó egyenes(ek) halad(nak) át ezen a ponton. Az ábrán is látszik, hogy ha \(\displaystyle P\) a sárga tartományba esik, akkor két egyenes halad át rajta, ha \(\displaystyle P\) a kék burkológörbén helyezkedik el, akkor csak egy (a burkolót érintő) egyenes halad át rajta, a fehér tartományba eső pontoknál pedig egyetlen \(\displaystyle \xi\) sem elégíti ki az (1) egyenletet. Fejezzük ki \(\displaystyle \xi\)-t (1)-ből:
| \(\displaystyle (2)\) | \(\displaystyle \xi^2+(y-x-h)\xi+xh=0.\) |
Ennek a másodfokú egyenletnek akkor van pontosan 1 megoldása, ha az egyenlet diszkriminánsa nulla:
\(\displaystyle (y-x-h)^2-4xh=0,\)
amit így is felírhatunk:
| \(\displaystyle (3)\) | \(\displaystyle 2h(x+y)=(y-x)^2+h^2.\) |
Belátjuk, hogy (3) egy olyan parabola egyenlete, amelynek szimmetriatengelye az \(\displaystyle x\) tengellyel \(\displaystyle 45^\circ\)-os szöget zár be.
Az \(\displaystyle (x,y)\) és a hozzá képest \(\displaystyle 45^\circ\)-kal elforgatott \(\displaystyle (X,Y)\) koordináta-rendszerek kapcsolata az 1. ábráról olvasható le:
\(\displaystyle X=\frac{x-y}{\sqrt2}, \qquad Y=\frac{x+y}{\sqrt2}.\)
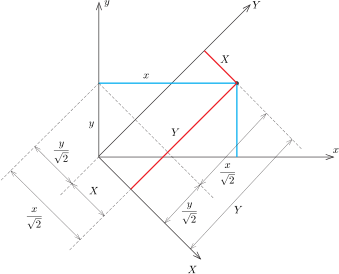
1. ábra
Ennek megfelelően a burkológörbe egyenlete:
| \(\displaystyle (4)\) | \(\displaystyle Y=\frac{1}{\sqrt2 h}X^2+\frac{h}{2\sqrt2},\) |
ami valóban egy parabolát ír le.
2. A test sebességének meghatározása.
A test kezdősebessége \(\displaystyle v_A=0.\) A \(\displaystyle \xi=h/2\) paraméterhez tartozó \(\displaystyle B\) pont koordinátái: \(\displaystyle x_B=y_B=h/4\), a \(\displaystyle \xi=h\) értéknek megfelelő \(\displaystyle C\) ponté pedig \(\displaystyle x_C=h\) és \(\displaystyle y_C=0\).
Írjuk fel az energiamegmaradás törvényét az \(\displaystyle A\) és \(\displaystyle B\), valamint az \(\displaystyle A\) és \(\displaystyle C\) pontok közötti mozgásra:
| \(\displaystyle (5)\) | \(\displaystyle \frac34mgh=\frac{1}{2}mv_B^2,\qquad \text{vagyis}\qquad v_B=\sqrt{\frac32gh},\) |
valamint
| \(\displaystyle (6)\) | \(\displaystyle mgh=\frac{1}{2}mv_C^2,\qquad \text{tehát}\qquad v_C=\sqrt{2gh}.\) |
3. Görbületi sugarak kiszámítása.
Egy síkgörbe simulókörének sugara (vagy ennek reciproka: a görbület) többféleképpen is meghatározható. Felsőbb matematikai módszerekkel (differenciálszámítással) a görbe egyenletéből közvetlenül megkaphatjuk a keresett sugár nagyságát, de elemi úton, fizikai (optikai vagy pontmechanikai) megfontolásokkal is célhoz érhetünk.
Tekintsük a feladatban szereplő elrendezést egy forgásparaboloid alakú tükör síkbeli metszetének (2. ábra).
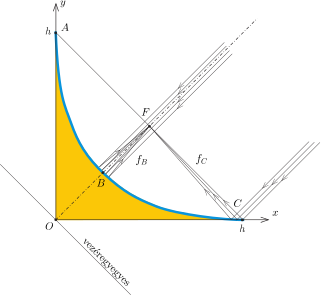
2. ábra
A tükör \(\displaystyle C\) pontjához érkező, a parabola tengelyével párhuzamos, tehát \(\displaystyle 45^\circ\)-os beesési szögű fénysugár \(\displaystyle 45^\circ\)-os szögben verődik vissza, az \(\displaystyle A\) pont irányába halad. Az optikai tengelyt a \(\displaystyle (h/2, h/2)\) koordinátájú \(\displaystyle F\) pontban éri el, ez a pont tehát a tükör fókuszpontja. A \(\displaystyle BF=f_B\) távolság \(\displaystyle h/2\sqrt{2}\), és – a gömbtükör ismert tulajdonságai miatt – ennek kétszerese a parabola görbületi sugara a \(\displaystyle B\) pontban:
| \(\displaystyle (7)\) | \(\displaystyle R_B=2f_B=\frac{h}{\sqrt2}.\) |
Megjegyzés. A parabola vezéregyenese az optikai tengelyre merőleges, tehát \(\displaystyle AC\)-vel párhuzamos, az origón áthaladó egyenes.
Hasonló megfontolásokkal kapjuk meg a \(\displaystyle C\) ponthoz tartozó görbületi sugár nagyságát is. A \(\displaystyle C\) közelébe érkező párhuzamos sugárnyaláb is az \(\displaystyle F\) pontban fókuszálódik, ilyen sugarakra tehát a fókusztávolság \(\displaystyle f_C=h/\sqrt2\). Egy \(\displaystyle R_C\) sugarú gömbtükörre nem merőlegesen, hanem \(\displaystyle \alpha\) beesési szögben érkező fénysugarakra a leképezési törvény:
\(\displaystyle \frac{1}{t}+\frac{1}{k}=\frac{2}{R_C\,\cos\alpha}\)
(lásd Kós Géza: Lehet egy közelítéssel kevesebb? c. cikkét a Kömal 2010. évi 3. számának 174-180. oldalán, http://db.komal.hu/KomalHU/). Esetünkben \(\displaystyle 1/t=0\), \(\displaystyle \alpha=45^\circ\) és \(\displaystyle k=f_C=h/\sqrt2\), ahonnan
| \(\displaystyle (8)\) | \(\displaystyle R_C=2h.\) |
(Nyilván ugyanekkora \(\displaystyle R_A\) is, de erre nincs szükségünk.)
A görbületi sugarakat nemcsak optikai megfontolásokkal, hanem a vízszintes hajítás képleteiből is megkaphatjuk. Fordítsuk el (és tükrözzük) az \(\displaystyle (X,Y)\) koordináta-rendszert úgy, hogy az \(\displaystyle Y\) tengely mutasson függőlegesen lefelé (3. ábra).
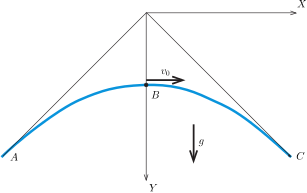
3. ábra
Tegyük fel a következő kérdést: Mekkora \(\displaystyle v_0\) nagyságú, vízszintes irányú kezdősebességgel kell elhajítanunk egy kicsiny testet, hogy annak pályagörbéje éppen a (4) egyenlettel megadott legyen? Mivel
\(\displaystyle X=v_0t \qquad \text{és}\qquad Y=\frac{h}{2\sqrt2}+\frac{g}2t^2,\)
a pálya egyenlete
\(\displaystyle Y= \frac{h}{2\sqrt2}+\frac{g}{2v_0^2} X^2. \)
Ezt (4)-gyel összevetve leolvashatjuk, hogy
\(\displaystyle v_0^2=\frac{gh}{\sqrt2}.\)
Tudjuk, hogy a test gyorsulása mindenhol \(\displaystyle g\), így a \(\displaystyle B\) pontban is, ami akkor egyezik meg a \(\displaystyle v_0^2/R_B\)-vel, ha \(\displaystyle R_B=h/\sqrt2\), ahogy azt már (7)-ben megkaptuk.
A \(\displaystyle C\) pontban, ahol a pályagörbe meredeksége \(\displaystyle -1\), a hajítás törvényei szerint \(\displaystyle v_C^2=\sqrt{2}gh\), a centripetális gyorsulása tehát
\(\displaystyle \frac{v_C^2}{R_C}=\frac{\sqrt2 gh}{R_C}=g\cos45^\circ=\frac{g}{\sqrt2}.\)
Innen kapjuk, hogy \(\displaystyle R_C=2h,\) összhangban (8)-cal.
4. A nyomóerők meghatározása.
Most, hogy ismerjük a test sebességét és a pálya görbületi sugarát a kritikus pontokban, könnyen kiszámíthatjuk a cső által kifejtett nyomóerőket is. Ha a pálya valamelyik pontjában a görbe normálisa (az érintőjére merőleges irány) \(\displaystyle \alpha\) szöget zár be a vízszintessel, a test sebessége \(\displaystyle v\) és a görbületi sugár \(\displaystyle R\), akkor (lásd a 4. ábrát) a Newton-egyenlet szerint
\(\displaystyle N-mg\cos\alpha=\frac{mv^2}{R},\)
vagyis
\(\displaystyle N=mg\cos\alpha+\frac{mv^2}{R}.\)
4. ábra
\(\displaystyle a)\) Az \(\displaystyle A\) pontnál \(\displaystyle \alpha=90^\circ\) és \(\displaystyle v_A=0\), így \(\displaystyle N_A=0.\)
\(\displaystyle b)\) A \(\displaystyle B\) pontnál \(\displaystyle \alpha=45^\circ\), \(\displaystyle v_B=\sqrt{\tfrac32gh}\) és \(\displaystyle R_B=\tfrac{h}{\sqrt2}\), ennek megfelelően \(\displaystyle N_B=2\sqrt2\,mg\approx 2{,}8\,mg\).
\(\displaystyle c)\) Végül a pálya legalsó, \(\displaystyle C\) pontjánál \(\displaystyle \alpha=0^\circ\), \(\displaystyle v_C=\sqrt{2gh}\) és \(\displaystyle R_C=2h\), így \(\displaystyle N_C=2mg\).
(Látható, hogy a nyomóerők és \(\displaystyle mg\) aránya nem függ \(\displaystyle h\) konkrét értékétől.) A fentebb kiszámított \(\displaystyle N\) erőket a cső fejti ki a lecsúszó testre. A kis test által a csőre kifejtett erők \(\displaystyle N\) ellenerejei.
Statistics:
24 students sent a solution. 6 points: Bencz Benedek, Csapó András, Csóka Péter, Czirják Márton Pál, Fajszi Karsa, Fehérvári Donát, Gyenes Károly, Képes Botond, Kiss 131 Adorján Timon, Tóth Kolos Barnabás. 3 points: 2 students. 1 point: 7 students. 0 point: 1 student.
Problems in Physics of KöMaL, December 2023
