Problem P. 5538. (January 2024)

P. 5538. In many playgrounds you will find a rotating climbing frame similar to the one in the figure. On such a climbing frame, an ant climbs up while the frame is rotating uniformly. The upward climbing ant constantly feels that it is climbing ``vertically upwards''.

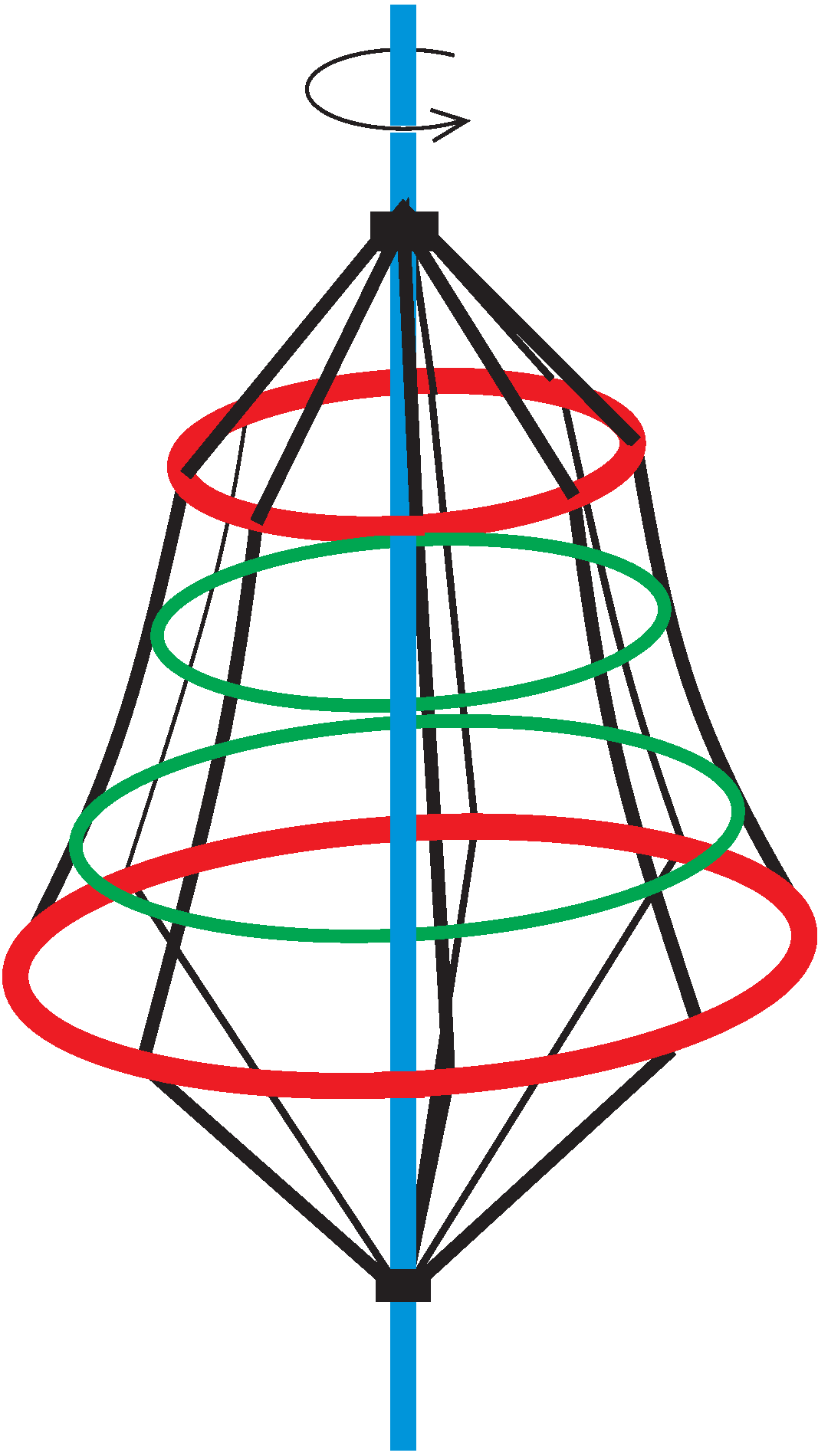
The radius of the lower red circular ring that hold the ropes of the climbing frame is \(\displaystyle 2~\text{m}\), whilst the upper red ring has a radius of \(\displaystyle 1~\text{m}\). The distance between the rings is \(\displaystyle 3~\text{m}\). What is the angular speed of the climbing frame?

(5 pont)

Deadline expired on February 15, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen az alsó merevítő gyűrű felett \(\displaystyle y\) magasságban a kötél távolsága a forgástengelytől \(\displaystyle r(y)\). Az \(\displaystyle m\) tömegű hangyára az \(\displaystyle \omega\) szögsebességgel forgó koordináta-rendszerben \(\displaystyle mg\) nagyságú, ,,valódi'' függőleges irányú nehézségi erő, valamint \(\displaystyle mr\omega^2\) nagyságú, vízszintes irányú centrifugális erő hat. Az eredő erő (a hangya által érzett nehézségi erő) párhuzamos a kötél érintőjével, tehát

\(\displaystyle \frac{mr\omega^2}{mg}=-\frac{\Delta r}{\Delta y}.\)

(\(\displaystyle \Delta r\) a forgómozgás pályasugarának kicsiny megváltozása, ha a forgástengellyel párhuzamos irányú elmozdulás egy kicsiny \(\displaystyle \Delta y\) érték.)

A fenti összefüggés szerint

\(\displaystyle \Delta r(y)=-\frac{\omega^2}{g}r(y)\cdot \Delta y.\)

Ez az egyenlet ugyanolyan alakú, mint a radioaktív bomlások \(\displaystyle \Delta m(t)=-\lambda m(t)\cdot \Delta t\) törvénye, ezért a megoldása analóg módon:

\(\displaystyle r(y)=r(0)\,\mathrm{e}^{-(\omega^2/g)y}.\)

A megadott számadatok szerint \(\displaystyle r(0)=2\,\mathrm{m}\), \(\displaystyle y=3\,\mathrm{m}\) és \(\displaystyle r(y)=1\,\mathrm{m}\), így

\(\displaystyle \omega=\sqrt{-\ln\left(\frac{r(y)}{r(0)}\right)\frac{g}{y}}=\sqrt{\ln 2\,\frac{9{,}8\,\mathrm{m/s^2}}{3\,\mathrm{m}}}=1{,}5\,\frac{1}{\mathrm{s}},\)

a fordulatszám pedig

\(\displaystyle f=\frac{\omega}{2\pi}=0{,}24\,\frac{1}{\mathrm{s}}.\)

A mászóka tehát kb. 4 másodpercenként fordul körbe.

Statistics:

15 students sent a solution.
5 points:	Czirják Márton Pál, Hegedüs Márk, Seprődi Barnabás Bendegúz.
4 points:	Csapó András, Kiss 131 Adorján Timon.
2 points:	1 student.
1 point:	3 students.
0 point:	5 students.

Problems in Physics of KöMaL, January 2024