Problem P. 5547. (February 2024)

P. 5547. A small wooden ball is attached to one end of a \(\displaystyle 30~\text{cm}\) long thread, and the free end of the thread is fixed to the bottom of a bucket at a distance of \(\displaystyle 20~\text{cm}\) from the centre. The bucket is filled with water and rotated around its axis of symmetry. (The water covers the ball during the motion.) What is the angular velocity at which the bucket must be spun so that after a long time the thread makes an angle of \(\displaystyle 30^\circ\) with the vertical?

(5 pont)

Deadline expired on March 18, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A feladat szövege szerint a vödör aljához rögzített fonál a függőlegessel \(\displaystyle 30^\circ\)-os szöget zár be, tehát megfeszül: ebből az következik, hogy a fagolyó sűrűsége kisebb a vízénél (erre következtethetünk az anyagából is). A golyóra a vízben a súlyerőn kívül a felhajtóerő is hat. A felhajtóerő nagysága a kiszorított víz súlyával egyenlő és azzal ellentétes irányú. A két erő eredője így szintén párhuzamos a súlyerővel, de mivel a felhajtóerő a nagyobb, így azzal ellentétes irányú. Ez alapján a fagolyót tartó fonál a forgás következtében a rögzítési ponton és a forgástengelyen átmenő síkban nem kifelé fog dőlni \(\displaystyle 30^\circ\)-kal (mintha levegőben forgatnánk), hanem befelé, így

\(\displaystyle r=(20-30\sin 30^\circ)=5\,\mathrm{cm}\)

távolságra lesz a forgástengelytől.

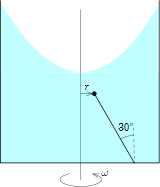
1. ábra

I. megoldás. A vödörrel együtt forgó vonatkoztatási rendszerben egy \(\displaystyle m\) tömegű, a forgástengelytől \(\displaystyle r\) távolságra lévő testre az \(\displaystyle mg\) nehézségi erőn kívül egy \(\displaystyle m\omega^2r\) nagyságú, a forgástengelyre merőleges, kifelé mutató centrifugális erő is hat. Ebben a rendszerben ennek a két erőnek az eredője a test súlya. Fogalmazhatunk úgy is, hogy a (helyfüggő) nehézségi gyorsulás itt \(\displaystyle \boldsymbol{g}'=\boldsymbol{g}+\omega^2\boldsymbol{r}\).

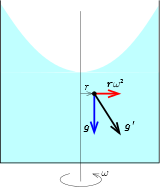
2. ábra

A bevezető gondolatmenet szerint a golyóra ható súlyerő és felhajtóerő eredője ezzel párhuzamos, de ellentétes irányú. Ezen kívül a forgó rendszerben nyugalomban lévő fagolyóra csak a fonálerő hat, így egyensúly csak akkor lehet ha az eredő súlyerő (és így a \(\displaystyle \boldsymbol{g}'\) nehézségi gyorsulás) párhuzamos a fonállal. Ez alapján

\(\displaystyle \frac{\omega^2r}{g}=\tg30^\circ,\)

és a keresett szögsebesség

\(\displaystyle \omega=\sqrt{\frac{g\tg30^\circ}{r}}=10{,}6\,\mathrm{\frac{1}{s}}.\)

II. megoldás. Inerciarendszerben a fagolyóra az \(\displaystyle m\boldsymbol{g}\) nehézségi erő, a víz által kifejtett \(\displaystyle \boldsymbol{F}_\mathrm{f}\) felhajtóerő és a \(\displaystyle \boldsymbol{K}\) kötélerő hat, ezek eredője tartja körpályán:

Milyen erőt fejt ki a forgó víz a golyóra? Érdemes végiggondolni, mi történik a nyugvó folyadékban. Ha a golyó helyén is folyadék lenne, akkor a körülötte lévő folyadék által kifejtett nyomóerők eredőjének a test helyén lévő folyadék súlyát kellene megtartania. Ezért a folyadékba helyezett testre is ugyanez az erő hat, ebből kapjuk meg, hogy a felhajtóerő nagysága a kiszorított folyadék súlyával egyenlő, és ellentétes irányú.

A forgó folyadékban a folyadék kicsiny, \(\displaystyle m_\mathrm{f}\) tömegű, a forgástengelytől \(\displaystyle r\) távolságra lévő darabja \(\displaystyle \omega^2r\) gyorsulással gyorsul a forgástengely felé. A kis folyadékdarab mozgásegyenlete így:

\(\displaystyle m_\mathrm{f}\boldsymbol{g}+\boldsymbol{F}_\mathrm{f}=-m_\mathrm{f}\omega^2\boldsymbol{r}.\)

Tehát ebben az esetben a körülötte lévő folyadéknak nem csak a folyadék \(\displaystyle m_\mathrm{f}g\) súlyát kell megtartania, hanem egy \(\displaystyle m_\mathrm{f}\omega^2r\) nagyságú, a forgástengely felé mutató vízszintes erőt is ki kell fejtenie. Ha a golyót ennek a kis folyadékdarabnak a helyére rakjuk, akkor arra is ugyanezzel az erővel hat a folyadék:

\(\displaystyle \boldsymbol{F}_\mathrm{f}=-m_\mathrm{f}(\boldsymbol{g}+\omega^2\boldsymbol{r}).\)

Ezt beírva az (1) egyenletbe:

\(\displaystyle m\boldsymbol{g}-m_\mathrm{f}(\boldsymbol{g}+\omega^2\boldsymbol{r})+\boldsymbol{K}=-m\omega^2\boldsymbol{r},\)

amiből:

\(\displaystyle \boldsymbol{K}=(m_\mathrm{f}-m)(\boldsymbol{g}+\omega^2\boldsymbol{r}).\)

A test folyadéknál kisebb sűrűsége miatt \(\displaystyle m_\mathrm{f}-m\) pozitív, tehát a \(\displaystyle \boldsymbol{K}\) kötélerő (és így a kötél is) párhuzamos a \(\displaystyle \boldsymbol{g}+\omega^2\boldsymbol{r}\) vektorral, ahogyan azt az előző megoldásban is láttuk. (A megoldás innen az előző gondolatmenettel adódik.)

Statistics:

45 students sent a solution.
5 points:	Csapó András, Czirják Márton Pál, Erős Fanni, Hornok Máté, Klement Tamás, Tóth Hanga Katalin, Vágó Botond.
4 points:	Nguyen Kim Dorka.
3 points:	6 students.
2 points:	5 students.
1 point:	13 students.
0 point:	9 students.

Problems in Physics of KöMaL, February 2024