 Problem P. 5548. (February 2024)
Problem P. 5548. (February 2024)
P. 5548. A small, flat fridge magnet weighs \(\displaystyle G\). The magnet is placed on the vertical side of the refrigerator and pulled in some direction in a vertical plane perpendicular to the plane of the metal side. The minimum force to move the magnet vertically upwards is \(\displaystyle F_1\) and the force to move it vertically downwards is \(\displaystyle F_2\).
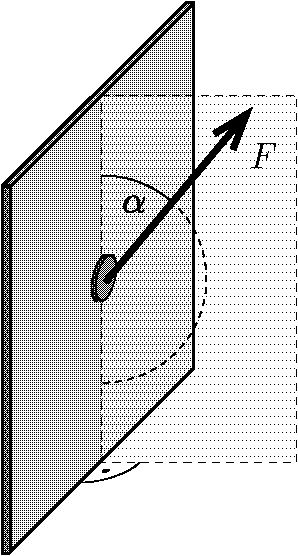
\(\displaystyle a)\) What is the coefficient of static friction between the side of the refrigerator and the magnet?
\(\displaystyle b)\) What is the force exerted by the metal side on the magnet, when the magnet is not pulled?
Data: \(\displaystyle G=0.10~\text{N}\), \(\displaystyle F_1=0.20~\text{N}\) and \(\displaystyle F_2=0.05~\text{N}\).
(See also the exercise numbered G. 702. in KöMal, issue 3, 2020.)
(5 pont)
Deadline expired on March 18, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük az általunk a mágnesre kifejtett \(\displaystyle \boldsymbol F\) erőnek a függőlegessel bezárt szögét \(\displaystyle \alpha\)-val, a mágnes és a fémlemez közötti vonzóerőt \(\displaystyle N\)-nel, a súrlódási együtthatót pedig \(\displaystyle \mu\)-vel. (Érdemes használni a súrlódási határszög fogalmát is a \(\displaystyle \mu=\tg\varepsilon\) definíciónak megfelelően.)
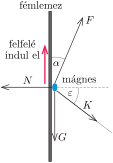
Ha a mágnes éppen megindul felfelé (1. ábra), akkor a fémlemez által kifejtett \(\displaystyle \boldsymbol{K}\) kényszererő függőlegesen lefelé mutató komponense (a súrlódási erő) a vízszintes erőkomponens (a nyomóerő) \(\displaystyle \mu\)-szöröse, az erőegyensúly feltétele tehát
\(\displaystyle \mu(N-F\sin\alpha)+G=F\cos\alpha,\)
vagyis
| \(\displaystyle (1)\) | \(\displaystyle F(\cos\alpha+\mu\sin\alpha)=\mu N+G.\) |
A fenti egyenlet szerint adott \(\displaystyle N\), \(\displaystyle G\) és \(\displaystyle \mu\) mellett \(\displaystyle F\) az \(\displaystyle \alpha\) szögtől függő mennyiség, amelynek legkisebb értékét keressük. \(\displaystyle F(\alpha)\) annál az \(\displaystyle \alpha\) szögnél a legkisebb, amelynél az (1)-ben szereplő zárójeles kifejezés a legnagyobb. Mivel
\(\displaystyle \cos\alpha+\mu\sin\alpha=\cos\alpha+\frac{\sin\varepsilon}{\cos\varepsilon}\sin\alpha=\frac{\cos(\alpha-\varepsilon)}{\cos\varepsilon,}\)
\(\displaystyle F(\alpha)\) legkisebb értéke az \(\displaystyle \alpha=\varepsilon\) szöghöz tartozik, nagysága
| \(\displaystyle (2)\) | \(\displaystyle F_1=(\mu N+G)\cos\varepsilon=N\sin\varepsilon+G\cos\varepsilon=\frac{\mu N+G}{\sqrt{1+\mu^2}}.\) |
Megjegyzés. \(\displaystyle \cos\alpha+\mu\sin\alpha\) szélsőértékét differenciálszámítással is megkaphatjuk:
\(\displaystyle (\cos\alpha+\mu\sin\alpha)'=-\sin\alpha+\mu\cos\alpha=0,\)
vagyis \(\displaystyle \mu=\tg\varepsilon=\tg\alpha,\) azaz \(\displaystyle \alpha=\varepsilon,\) és a maximum nagysága
\(\displaystyle (\cos\alpha+\mu\sin\alpha)_\text{max.}=\cos\varepsilon+\frac{\sin^2\varepsilon}{\cos\varepsilon}=\frac{1}{\cos\varepsilon}.\)
 \(\displaystyle \qquad\qquad\)
\(\displaystyle \qquad\qquad\)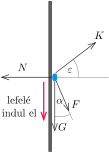
1. ábra\(\displaystyle \qquad\qquad\qquad\qquad\qquad\)2. ábra
Hasonló lépésekkel kaphatjuk meg, hogy a lefelé éppen meginduló mágnesre fennálló összefüggéseket is (2. ábra). Ha a külső \(\displaystyle \boldsymbol{F}\) erő ferdén lefelé, a függőlegessel \(\displaystyle \alpha\) szögben hat, akkor
\(\displaystyle \mu(N-F\sin\alpha) =F\cos\alpha+G,\)
vagyis
| \(\displaystyle (3)\) | \(\displaystyle F(\cos\alpha+\mu\sin\alpha)=\mu N-G.\) |
(Külső erő hiányában a mágnes nem csúszik le, tehát \(\displaystyle \mu N\ge G\), és így (3) jobb oldala nemnegatív.)
A (3)-ban szereplő \(\displaystyle F\) szélsőértéke ugyancsak \(\displaystyle \alpha=\varepsilon\)-nál lesz, és a minimum
| \(\displaystyle (4)\) | \(\displaystyle F_2=(\mu N-G)\cos\varepsilon=N\sin\varepsilon-G\cos\varepsilon=\frac{\mu N-G}{\sqrt{1+\mu^2}}.\) |
A továbbiak szempontjából fontos (2) és (4) összefüggéseket egyszerűbben, geometriai szerkesztéssel is megkaphatjuk. Tételezzük fel, hogy a mágnes felfelé indul el (3. ábra).
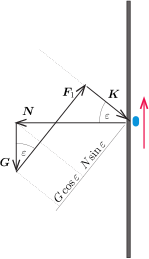
3. ábra
A testre négyféle erő hat: a fémlemez által kifejtett \(\displaystyle \boldsymbol{N}\) mágneses vonzóerő, a testre ható \(\displaystyle \boldsymbol{G}\) nehézségi erő, az általunk kifejtett \(\displaystyle \boldsymbol{F}\) erő és a lemez által kifejtett \(\displaystyle \boldsymbol{K}\) mechanikai kényszererő. Ez a négy erő (ha egymás után mérjük fel azokat) zárt vektorpoligont alkot, vektori összegük nulla. \(\displaystyle \boldsymbol{N}\)-et és \(\displaystyle \boldsymbol{G}\)-t ismertnek vehetjük (jóllehet \(\displaystyle N\) nagyságát majd csak később fogjuk megkapni), \(\displaystyle \boldsymbol{K}\)-nak csak az irányát tudjuk: a vízszintessel \(\displaystyle \varepsilon\) szöget zár be és ferdén lefelé mutat. Az általunk kifejtett \(\displaystyle \boldsymbol{F}\) erők közül azt az \(\displaystyle \boldsymbol{F}_1\)-et keressük, amelyiknek a nagysága (hossza) a legkisebb. Az ábráról leolvasható, hogy a minimumot akkor kapjuk, amikor \(\displaystyle \boldsymbol{F}=\boldsymbol{F}_1\) merőleges \(\displaystyle \boldsymbol{K}\)-ra, vagyis a hatásvonala a függőlegessel \(\displaystyle \varepsilon\) nagyságú szöget zár be. Látszik, hogy ilyenkor
\(\displaystyle F_1=N\sin\varepsilon+G\cos\varepsilon,\)
ami éppen a korábban megkapott (2) összefüggés.
Hasonló módon szerkeszthetjük meg a lefelé mozdításhoz szükséges legkisebb \(\displaystyle \boldsymbol{F}=\boldsymbol{F}_2\) erőt is (4. ábra).
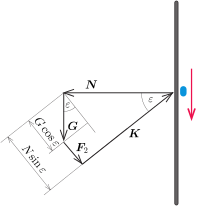
4. ábra
A \(\displaystyle \boldsymbol{K}\) erő most ferdén felfelé mutat, a hatásvonala \(\displaystyle \varepsilon\) szöget zár be a vízszintessel. Az ábráról leolvashatjuk, hogy a legkisebb külső erő nagysága
\(\displaystyle F_2=N\sin\varepsilon-G\cos\varepsilon,\)
összhangban a korábban megkapott (4) összefüggéssel.
Visszatérve a feladat eredeti kérdéseihez, most már könnyen megadhatjuk a keresett \(\displaystyle N\) és \(\displaystyle \mu\) értékeket.
\(\displaystyle a)\) (2) és (4) különbségét képezve
\(\displaystyle F_1-F_2=2G\cos\varepsilon,\)
vagyis
\(\displaystyle \varepsilon=\arccos\frac{F_1-F_2}{2G}=\arccos\frac{0{,}20-0{,}05 }{2\cdot0{,}10}=\arccos 0{,}75=41{,}4^\circ,\)
\(\displaystyle \mu=\tg 41{,}4^\circ=0{,}88\approx 0{,}9.\)
\(\displaystyle b)\) (2) és (4) összegéből kapjuk:
\(\displaystyle N=\frac{F_1+F_2}{2\sin\varepsilon}\approx 0{,}19\,\mathrm{N}.\)
Statistics:
35 students sent a solution. 5 points: Bencze Mátyás, Csiszár András, Csóka Péter, Czirják Márton Pál, Fajszi Karsa, Fehérvári Donát, Gyenes Károly, Hegedüs Márk, Kiss 131 Adorján Timon, Masa Barnabás, Seprődi Barnabás Bendegúz, Simon János Dániel, Sütő Áron, Szabó Donát, Tóth Hanga Katalin, Zólomy Csanád Zsolt. 4 points: Molnár Ábel, Tóth Kolos Barnabás. 3 points: 3 students. 2 points: 3 students. 1 point: 1 student. 0 point: 5 students. Not shown because of missing birth date or parental permission: 1 solutions.
Problems in Physics of KöMaL, February 2024
