 Problem P. 5549. (February 2024)
Problem P. 5549. (February 2024)
P. 5549. We bend a closed planar curve from a piece of thin wire of uniform mass distribution and of mass \(\displaystyle M\). The moment of inertia of the resulting frame is \(\displaystyle \Theta_0\) with respect to an axis which passes through the centre of mass and is perpendicular to its plane. The frame is then subjected to an experiment as shown in the figure (the centre of mass is denoted with the letter combination ``TKP"): the frame is suspended at various points and the period of its small amplitude oscillations in its own plane is measured. What is the minimum possible period of the oscillation?
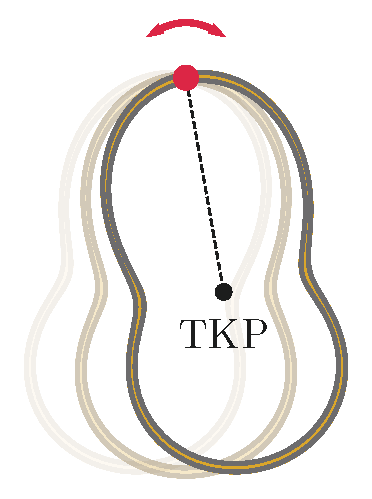
(5 pont)
Deadline expired on March 18, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsünk egy tetszőleges felfüggesztési pontot, jelölje ennek a keret tömegközéppontjától mért távolságát \(\displaystyle s\), a test erre vonatkozó tehetetlenségi nyomatékát \(\displaystyle \Theta_s\). Utóbbi kapcsolatba hozható a tömegközépponti tehetetlenségi nyomatékkal a \(\displaystyle \Theta_s=\Theta_0+Ms^2\) Steiner-tétel által. Ezt felhasználva, a kiválasztott tengelyhez tartozó lengésidő az alábbi alakot ölti:
| \(\displaystyle (1)\) | \(\displaystyle T_s=2\pi\sqrt{\frac{\Theta_s}{Mgs}}=2\pi\sqrt{\frac{\Theta_0}{Mgs}+\frac{s}{g}}.\) |
A gyök alatti kifejezés alulról becsülhető a számtani és mértani közepek közötti egyenlőtlenség segítségével:
\(\displaystyle \frac{\Theta_0}{Mgs}+\frac{s}{g}\ge\sqrt{\frac{4\Theta_0}{Mg^2}}.\)
Egyenlőség akkor lép fel, amikor a két tag megegyezik; ez a feltétel az alábbi speciális \(\displaystyle s_\mathrm{min}\) érték esetén teljesül, amelyet az 1. ábrán is vázoltunk:
\(\displaystyle s_\mathrm{min}=\sqrt{\frac{\Theta_0}{M}}.\)
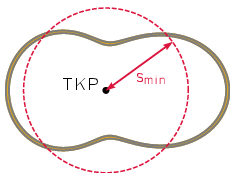
1. ábra
Kérdés, hogy van-e olyan pontja a keretnek, amely a tömegközépponttól éppen ekkora távolságra esik. Hogy ezt megválaszoljuk, érdemes a tehetetlenségi nyomaték definícióját felhasználva \(\displaystyle s_\mathrm{min}\) négyzetét szemléletesebb alakra hozni:
| \(\displaystyle (2)\) | \(\displaystyle s_\mathrm{min}^2=\frac{\sum_{i}m_is_i^2}{\sum_im_i}=\langle s^2\rangle,\) |
azaz \(\displaystyle s_\mathrm{min}\) éppen a huzal egyes pontjaihoz tartozó \(\displaystyle s\) távolságok négyzetes közepe. Mivel a középérték biztosan a legkisebb és legnagyobb távolságok közé esik, a huzal folytonossága miatt annak biztosan lesz legalább egy pontja, amely \(\displaystyle s_\mathrm{min}\) távol helyezkedik el a tömegközépponttól. Az ehhez tartozó minimális \(\displaystyle T_\mathrm{min}\) lengésidő az (1) egyenlethez visszatérve kiszámítható:
\(\displaystyle T_\mathrm{min}=2\pi\sqrt[4]{\frac{4\Theta_0}{Mg^2}}.\)
Végeredményben tehát ez lesz a mért lengésidők minimuma.
Megjegyzés. Érdekesség, hogy a (2) egyenletből nem csupán az következik, hogy a huroknak legalább egy pontja a tömegközépponttól \(\displaystyle s_\mathrm{min}\) távolságra esik, hanem az is, hogy legalább kettő. Ennek oka, hogy a hurok zárt, így bármely metszésponthoz, ahol a huzal az 1. ábrán jelölt körbe belép, kell tartoznia egy másik pontnak is, ahol kilép. Egyetlen érintési pont nem jöhet létre, hiszen a huzal nem lehet teljes egészében sem a körön belül, sem azon kívül. A két minimális lengésidejű pont esetére konstrukció is adható, például a 2. ábrán látható patkószerű hurok.
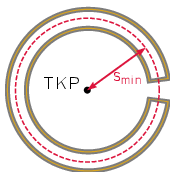
2. ábra
Statistics:
32 students sent a solution. 5 points: Czirják Márton Pál, Gyenes Károly, Pázmándi József Áron. 4 points: Bencz Benedek, Bernhardt Dávid, Csiszár András, Csóka Péter, Debreceni Dániel, Dobos Anita, Fajszi Karsa, Fehérvári Donát, Gerendás Roland, Kiss 131 Adorján Timon, Klement Tamás, Masa Barnabás, Nguyen Kim Dorka, Simon János Dániel, Sütő Áron, Szabó Donát, Tóth Hanga Katalin, Tóth Kolos Barnabás. 3 points: 1 student. 2 points: 2 students. 0 point: 5 students.
Problems in Physics of KöMaL, February 2024
