 Problem P. 5552. (February 2024)
Problem P. 5552. (February 2024)
P. 5552. Imagine that power \(\displaystyle P\) is delivered through the coaxial cable of length \(\displaystyle \ell\) as shown in the figure. The radius of the inner conductor of the cable, which has negligible resistance, is \(\displaystyle a\), and the radius of the thin-walled outer tube, which can be considered to have similarly negligible resistance, is \(\displaystyle b\). There is a vacuum both outside the cable and between the inner conductor and the outer tube, and a direct current flows through the cable.
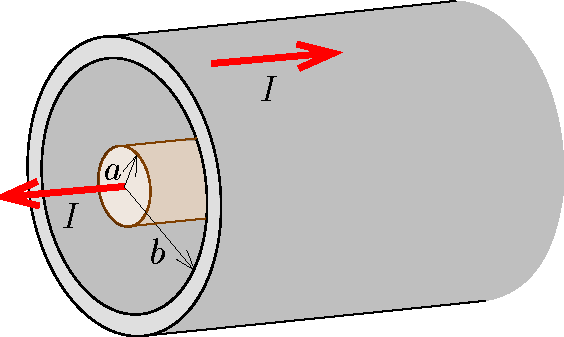
\(\displaystyle a)\) What is the value of the current if there is no outward and inward force exerted on the outer tube?
\(\displaystyle b)\) At which end of the coaxial cable – left or right – is the generator (voltage supply) and at which end is the resistor (load)?
(6 pont)
Deadline expired on March 18, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a\)) Mivel a vezeték ellenállásmentes, a rajta folyó áram ellenére nem esik rajta feszültség, és a két vezeték között, a vezeték mentén mindenhol ugyanakkora a feszültség. Ezt a vezetékek felületére kiült töltések biztosítják. A két vezeték töltése ellentétes, ezért vonzzák egymást. Ugyanakkor a két vezetékben az áram ellentétes irányú, ez egy taszítást eredményez. A vizsgált esetben ez a két hatás éppen kompenzálja egymást.
Foglalkozzunk először az elektrosztatikus vonzással! Legyen mondjuk a belső vezeték felszíne pozitív, ennek megfelelően a cső (mivel a kettő együtt semleges) negatív töltésű. Az elektromos térerősséget egy, a két vezeték között elhelyezkedő, azokkal koaxiális \(\displaystyle r\) sugarú henger felületén a Gauss-tételből határozhatjuk meg:
\(\displaystyle E(r)=\frac{1}{\varepsilon _0}\frac{Q}{2\pi r\ell}=\frac{1}{\varepsilon _0}\frac{\varrho_aa}{r},\)
ahol \(\displaystyle \varrho_a\)-val jelöltük a belső vezeték felületi töltéssűrűségét. \(\displaystyle E(r)\), megegyezésben a belső vezetéken lévő töltések előjelével, pozitív, ha kifelé mutat. A cső belső falára ugyanannyi, de ellentétes előjelű töltés ül ki, mint a belső vezetékre, ezért ott a felületi töltéssűrűség
\(\displaystyle \varrho_b=-\frac{a\varrho_a}{b}.\)
Ennek megfelelően a cső belső falánál (azaz a tengelytől \(\displaystyle b\) távolságra) a térerősség
\(\displaystyle E(b)=\frac{1}{\varepsilon _0}\frac{\varrho_a a}{b}=-\frac{1}{\varepsilon _0}\varrho_b,\)
míg a külső falánál nyilván nulla, a két érték között pedig valamilyen \(\displaystyle E(z)\) függvény szerint cseng le. A felületi (a felület közelében sűrűsödő) töltésekre ható erőt az alábbi megfontolásokkal számíthatjuk ki. Tekintsük a cső falának egy kicsiny \(\displaystyle \Delta{l}\) szélességű (gyűrűszerű) darabját, és osszuk fel a falvastagságnál jóval vékonyabb \(\displaystyle \Delta{z}\) vastagságú rétegekre úgy, hogy a \(\displaystyle z_n=b+n\Delta{z}\) értékek közül a \(\displaystyle z_{N}\) már olyan távol legyen a belső faltól, hogy ott a térerő már eltűnjön! (\(\displaystyle z_N\) eshet pl. a cső külső falára.) A Gauss-tétel szerint a \(\displaystyle z_{n-1}\) és \(\displaystyle z_n\) közötti rész töltése
\(\displaystyle q_n=\varepsilon_0\left(2\pi z_n E(z_n)-2\pi z_{n-1}E(z_{n-1})\right)\Delta{l}.\)
Mivel a cső fala a sugarához képest vékony, nem követünk el lényeges hibát, ha a térerősségek előtt álló \(\displaystyle z_{{n}-1}\) és \(\displaystyle z_{n}\) változókat \(\displaystyle b\)-nek vesszük, és csak a cső falában gyorsan nullára csökkenő \(\displaystyle E(z)\) argumentumában hagyjuk meg változónak:
\(\displaystyle q_{n}=\varepsilon_02\pi b\left(E(z_n)-E(z_{n-1})\right)\Delta{l}.\)
A gyűrű egy kicsiny \(\displaystyle \Delta d\) hosszúságú ívére eső összes töltésre ható erő
\(\displaystyle F=\sum_{n=0}^{n=N}q_n\frac{\Delta d}{2\pi b}\overline{E}_n,\)
ahol \(\displaystyle \overline{E}_n\) az átlagos térerősség az \(\displaystyle n\)-edik rétegben. Nagyon jó közelítés, ha ennek a két szélső érték számtani közepét vesszük, azaz az \(\displaystyle \overline{E}_n={(E(z_n)+E(z_{n-1}))}/{2}\) értékkel számolunk. Mindent behelyettesítve a cső falának \(\displaystyle \Delta l\cdot\Delta d\) nagyságú darabján levő összes töltésre ható erő
\(\displaystyle F=\sum_{n=0}^{n=N}\varepsilon_0\frac{E^2(z_n)-E^2(z_{n-1})}{2}\Delta{l}\Delta{d}=\varepsilon_0\frac{E^2(z_N)-E^2(z_0)}{2}\Delta{l}\Delta{d},\)
ami az \(\displaystyle E(z_0)=E(b)=-\varrho_b/\varepsilon_0\) és \(\displaystyle E(z_N)=0\) miatt
\(\displaystyle F=-\frac{\varrho_b^2}{2\varepsilon_0}\Delta{l}\Delta{d}.\)
Ennek megfelelően egy egységnyi felületű darabot a töltések vonzása miatt
\(\displaystyle \sigma_\mathrm{el.}=\frac{\varrho_b^2}{2\varepsilon_0}\)
nagyságú erő húz befelé. (Ez hatását tekintve olyan, mint egy ,,negatív nyomás".)
Megjegyzés. Számolásunkban csak azt használtuk ki, hogy a töltések a henger sugarához képest vékony rétegben helyezkednek el, így nem kellett figyelembe vennünk a térerősségnek a geometriából (\(\displaystyle r\) növekedéséből) adódó csökkenését. Nem volt szükségünk a ténylegesen kialakuló töltéseloszlás alakjára, ez így tehát a töltött fémfelületekre általánosan használható eredmény: ha egy sima (kis görbületű) felületű fém felületi töltéssűrűsége valahol \(\displaystyle \varrho_f\), akkor ott az egységnyi felületre \(\displaystyle \sigma={\varrho_f^2}/{2\varepsilon_0}\) erő hat kifelé, és ettől eltérés csak élek és csúcsok közelében lehet.
A közvetlenül nem mérhető \(\displaystyle \varrho_b\) felületi töltéssűrűség helyett érdemes a \(\displaystyle \sigma\)-t a vezetékek közötti \(\displaystyle U\) elektromos feszültséggel kifejezni. A koaxiális kábel lényegében egy hengerkondenzátornak tekinthető, aminek a kapacitása
\(\displaystyle C=\frac{2\pi\varepsilon_0\ell}{\ln{(b/a)}}.\)
Ennek a kapacitásnak a teljes töltése
\(\displaystyle Q=2\pi{b}\ell|\varrho_b|,\)
ami megadható a feszültséggel is:
\(\displaystyle Q=CU={\frac{2\pi\varepsilon_0\ell}{\ln\left(\frac{b}{a}\right)}}U.\)
A két kifejezés egybevetéséből kapott \(\displaystyle |\varrho_b|\) behelyettesítésével
\(\displaystyle \sigma_\mathrm{el.}=\frac{\varepsilon _0}{2b^2}\frac{U^2}{\left(\ln\frac{b}{a}\right)^2}.\)
Megjegyzés. Ha nem ismernénk a hengerkondenzátor kapacitásának képletét, a belső és külső vezeték közötti feszültség meghatározásához a két vezeték közötti elektromos térerősséget kellene a kicsiny \(\displaystyle \Delta r\) szakaszokra osztott \(\displaystyle a\leq r\leq b\) intervallumra felösszegeznünk:
\(\displaystyle U=\sum E(r)\Delta{r}=\frac{\varrho_aa}{\varepsilon_0}\sum\frac{\Delta r}{r}.\)
Az összegzés (integrálás) eredményét megtalálhatjuk a ,,Négyjegyű függvénytáblázatban'' a Fontosabb integrálok között, de kihasználhatjuk azt is, hogy ez matematikai szempontból ugyanaz a feladat, mint pl. az ideális gáz állandó hőmérsékleten végzett munkája, miközben \(\displaystyle V_1\)-ről \(\displaystyle V_2\) térfogara tágul, és aminek az eredményét ismerjük:
\(\displaystyle W=\sum p\Delta V=nRT\sum\frac{\Delta V}{V}=nRT\ln{\frac{V_2}{V_1}}.\)
Az analógia, felhasználva, hogy \(\displaystyle a|\varrho_a|=b|\varrho_b|\), az
\(\displaystyle U=\frac{\vert\varrho_b\vert b}{\varepsilon _0}\ln{\frac{b}{a}}\)
összefüggésre vezet, ami természetesen ugyanaz, mint amit a hengerkondenzátor kapacitása alapján kapunk.
A mágneses erők kiszámításánál a fentiekhez hasonló módon kell eljárnunk. A belső vezetékben folyó \(\displaystyle I\) áram mágneses indukciója a cső belső falánál
\(\displaystyle B=\mu _0\frac{I}{2\pi b},\)
ami a külső vezetéken folyó ugyancsak \(\displaystyle I\) nagyságú, de ellentétes irányú áram hatására fokozatosan nullára csökken. Az előzőekhez hasonlóan osszuk fel a külső vezetéket \(\displaystyle N\) darab \(\displaystyle \Delta z\) vastagságú rétegre! A \(\displaystyle z_n=b+n\Delta z\) és a \(\displaystyle z_{n-1}=b+(n-1)\Delta z\) közötti rétegben folyó \(\displaystyle I_n\) áramra igaz, hogy
\(\displaystyle 2\pi z_{n-1}B(z_{n-1})-2\pi z_nB(z_n)=\mu_0 I_n.\)
(Itt az egyes mennyiségek akkor pozitívok, ha megfelelnek az ábrának és a jobbkéz-szabálynak.) Mivel a cső fala vékony a sugarához képest (ahogy a töltésekre vonatkozó számolás esetében is), a \(\displaystyle z_n\) értékeket mindenhol \(\displaystyle b\)-nek vehetjük, ahol nem gyorsan változó függvény változójáról van szó, így
\(\displaystyle I_n=\frac{2\pi b(B(z_{n-1})-B(z_n))}{\mu_0}.\)
Ennek megfelelően az \(\displaystyle n\)-edik réteg keskeny, \(\displaystyle \Delta d\) szélességű, a tengellyel párhuzamos sávjában
\(\displaystyle \frac{\Delta d}{2\pi b}I_n=\frac{(B(z_{n-1})-B(z_n))}{\mu_0}\Delta d\)
áram folyik. Ennek egy \(\displaystyle l\) hosszúságú szakaszára az átlagosan
\(\displaystyle \frac{(B(z_{n-1})+B(z_n))}{2}\)
mágneses indukció miatt
\(\displaystyle F_n=\frac{\Delta d}{2\pi b}I_nl\frac{(B(z_{n-1})+B(z_n))}{2}=\frac{(B^2(z_{n-1})-B^2(z_n))}{2\mu_0}l\Delta d\)
erő hat. Ezek összege megadja a cső falának egy \(\displaystyle \Delta d\) széles, \(\displaystyle l\) hosszú darabjára ható \(\displaystyle F\) erőt:
\(\displaystyle F=\sum_{n=0}^{n=N}F_n=\frac{l\Delta d}{2\mu_0}\sum_{n=0}^{n=N}(B^2(z_{n-1})-B^2(z_n))=\frac{(B^2(z_0)-B^2(z_N))}{2\mu_0}l\Delta d.\)
Tekintettel arra, hogy
\(\displaystyle B(z_0)=\mu _0\frac{I}{2\pi b}\qquad\textrm{és}\qquad B(z_N)=0,\)
\(\displaystyle F=l\Delta d \frac{\mu_0I^2}{8\pi^2b^2},\)
tehát az ellentétes irányú áramok taszítása miatt a cső falának egy egységnyi területű darabját
\(\displaystyle \sigma_\mathrm{mágn.}=\mu_0\frac{I^2}{8\pi^2b^2}\)
nagyságú erő igyekszik kifelé tolni.
Megjegyzés. Sok évtizede próbálkoznak az elektromos energia nagy távolságokra történő, veszteség nélküli szállításának megvalósításával szupravezető kábeleken. A szupravezetőkre nem csak az jellemző, hogy az áramot ellenállás mentesen képesek vezetni, hanem az is, hogy kiszorítják magukból a mágneses teret (Meissner-effektus). Ez azt jelenti, hogy a mágneses tér a szupravezető felületétől befelé indulva egy nagyon keskeny sávon belül lecseng. Értelemszerűen áram is csak ebben a sávban folyhat, különben a tér nem lehetne nulla a szupravezető belsejében. Számolásunk eredménye, lévén független a mágneses tér tényleges alakjától, erre az esetre is érvényes.
Feladatunk szerint a kétféle erőhatás éppen kompenzálja egymást, azaz
\(\displaystyle \mu_0\frac{I^2}{8\pi^2b^2}=\frac{\varepsilon _0}{2b^2}\frac{U^2}{\left(\ln\frac{b}{a}\right)^2},\)
amiből meghatározhatjuk (talán kissé váratlanul) a terhelés (fogyasztó) ellenállását:
\(\displaystyle R=\frac{U}{I}=\frac{1}{2\pi}\sqrt{\frac{\mu _0}{\varepsilon _0}}\ln\frac{b}{a}.\)
Tudjuk a távvezeték által szállított másodpercenkénti energiát: \(\displaystyle P=RI^2\), így a kérdéses áramerősség is meghatározható:
\(\displaystyle I=\sqrt{\frac{P}{R}}=\sqrt{2\pi P\left(\ln\frac{b}{a}\right)^{-1}\sqrt{\frac{\varepsilon_0}{\mu_0}}}.\)
\(\displaystyle b\)) Egy egyszerű, tápegységből, fogyasztóból és a megfelelő vezetékekből álló áramkörre igaz, hogy a fogyasztóban az áram a magasabb potenciálú hely felől az alacsonyabb potenciálú felé folyik, míg a tápegységben ez pont fordítva van. Ha a középső vezeték pozitív töltésű, akkor balra kell lennie a fogyasztónak jobbra pedig a generátornak, míg ha a külső cső pozitív, akkor éppen fordítva.
Megjegyzések. 1. Meghatározhatjuk a távvezeték feszültségét (\(\displaystyle U={P}/{I}\)), sőt a belső vezetéken, illetve a cső belső felületén felhalmozódó töltést is (\(\displaystyle Q={{2\pi\varepsilon _0\ell}/{\ln{\left(\tfrac{b}{a}\right)}U}}\)).
2. A szállított energia a belső vezeték és a külső cső közötti vákuumozott térben terjed, és az energiaáram-sűrűséget az
\(\displaystyle \boldsymbol{S}=\frac{1}{\mu_0}\boldsymbol{E}\times\boldsymbol{B}\)
Poynting-vektor határozza meg. Ha a középső vezeték pozitív töltésű, akkor ez az ábrán balra mutat, összhangban azzal, hogy ekkor a fogyasztónak balra kell lennie, viszont ha a külső vezeték a pozitív, a helyzet fordított. A Poynting-vektor nagysága
\(\displaystyle S(r)=\frac{1}{\mu_0}\,\vert\boldsymbol{E}\times\boldsymbol{B}\vert=\frac{1}{\mu_0}\left(\frac{1}{\varepsilon_0}\frac{Q}{2\pi r\ell}\right)\left(\mu_0\frac{I}{2\pi r}\right)=\frac{1}{\varepsilon_0}\frac{QI}{4\pi^2\ell}\,\frac{1}{r^2}=\frac{UI}{2\pi}{\left(\ln\frac{b}{a}\right)^{-1}}\frac{1}{r^2}.\)
Ennek alapján egy \(\displaystyle r\) sugarú \(\displaystyle \Delta r\) szélességű sávban
\(\displaystyle 2\pi r\Delta rS(r)={UI}{\left(\ln\frac{b}{a}\right)^{-1}}\frac{\Delta r}{r}\)
energia áramlik. Ezt felösszegezve a teljes \(\displaystyle a\leq r \leq b\) sávra megkapjuk az elvárásainknak megfelelő \(\displaystyle P=UI\) eredményt.
Statistics:
7 students sent a solution. 6 points: Klement Tamás. 5 points: Bencz Benedek, Czirják Márton Pál, Tóth Kolos Barnabás. 1 point: 1 student. 0 point: 1 student.
Problems in Physics of KöMaL, February 2024
