 Problem P. 5557. (March 2024)
Problem P. 5557. (March 2024)
P. 5557. A cylinder of mass \(\displaystyle m\), radius \(\displaystyle r\), and with a uniform mass distribution, rolls back and forth without sliding inside a fixed, thin-walled tube of radius \(\displaystyle R\), near the lowest point of the tube. What is the period of the motion?
(5 pont)
Deadline expired on April 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Jellemezzük a henger (görgő) helyzetét a tengely oldalirányú kitérésének \(\displaystyle \phi\), és a tengely körüli elfordulás \(\displaystyle \varphi\) szögével!
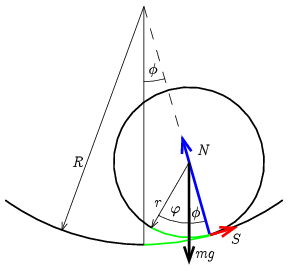
A kettő nem független, tiszta gördülés esetén (az ábrán a két zöld körív hossza megegyezik)
\(\displaystyle R\phi=r(\varphi+\phi),\qquad\textrm{azaz}\qquad\varphi=\frac{R-r}{r}\phi.\)
Analóg összefüggés igaz a megfelelő szögsebességekre, illetve a nekünk fontos \(\displaystyle \beta_{\varphi}\) és \(\displaystyle \beta_{\phi}\) szöggyorsulásokra is:
\(\displaystyle \beta_{\varphi}=\frac{R-r}{r}\beta_{\phi}.\)
Adott \(\displaystyle \phi\) mellett a henger tengelye a cső legmélyebb pontjához képest
\(\displaystyle y=r+(R-r)(1-\cos \phi)\)
magasságban van, és az alaphelyzettől
\(\displaystyle x=(R-r)\sin{\phi}\)
vízszintes távolságra tér ki oldalra.
Jelölje \(\displaystyle N\) a görgő és a cső fala közötti nyomó, \(\displaystyle S\) pedig a súrlódási erőt! Ha \(\displaystyle a_y\) és \(\displaystyle a_x\) a tömegközéppont függőleges illetve vízszintes gyorsulása, akkor a mozgás dinamikáját leíró egyenletek
$$\begin{align*} ma_y &=N\cos{\phi}+S\sin{\phi}-mg,\\ ma_x &=-N\sin{\phi}+S\cos{\phi},\\ \theta\beta_{\varphi} &=-rS, \end{align*}$$ahol \(\displaystyle \theta\) a görgőnek a szimmetriatengelyére vonatkozó tehetetlenségi nyomatéka.
Kis kitérések esetén, amikor jó közelítés, hogy \(\displaystyle \sin\phi\cong \phi\) és \(\displaystyle \cos{\phi} \cong 1\), \(\displaystyle y=r\)-nek, így \(\displaystyle a_y=0\)-nak vehető, a vízszintes gyorsulás pedig (mivel \(\displaystyle x\cong (R-r){\phi}\)) az
\(\displaystyle a_x=(R-r)\beta_{\phi}\)
kifejezéssel közelíthető. Végső soron a mozgásegyenletek az
$$\begin{align*} N &=mg-S\phi,\\ m(R-r)\beta_{\phi} &=-N{\phi}+S,\\ \theta\beta_{\varphi} &=-rS \end{align*}$$egyenletekre redukálódnak. Ezekből a \(\displaystyle \beta\)-kra vonatkozó kényszer mellett az \(\displaystyle N\) és az \(\displaystyle S\) kiküszöbölése és \(\displaystyle \phi^2\ll 1\) felhasználása után a
\(\displaystyle \beta_{\phi}=-\frac{g}{(1+\theta/mr^2)(R-r)}\phi\)
összefüggés adódik. Ebből leolvasható, hogy a rezgés körfrekvenciája
\(\displaystyle \omega=\sqrt{\frac{g}{(1+\theta/mr^2)(R-r)}},\)
tehát a periódusideje
\(\displaystyle T=\frac{2\pi}{\omega}=2\pi\sqrt{\left(1+\frac{\theta}{mr^2}\right)\frac{R-r}{g}}.\)
Homogén tömör görgő esetén \(\displaystyle \theta=mr^2/2\), így
\(\displaystyle T=2\pi\sqrt{\frac{3}{2}\frac{R-r}{g}}.\)
Megjegyzés. Vegyük észre, hogy a ,,kis kitérés'' követelménye csak a \(\displaystyle \phi\)-re vonatkozik (ennek a szögfüggvényei esetében éltünk közelítéssel), de kicsi \(\displaystyle \phi\)-hez tartozhat akár nagy \(\displaystyle \varphi\) is (ha \(\displaystyle R\gg r\)).
II. megoldás. Használjuk az I. megoldás jelöléseit és a tapadásból következő
\(\displaystyle \beta_\varphi=\frac{R-r}{r}\beta_\phi\)
összefüggést. Írjuk fel a gördülő hengerre a forgómozgás alapegyenletét a pillanatnyi forgástengelyre (a két henger \(\displaystyle C\) érintkezési pontjára) vonatkoztatva! Ezt általában nem lehet megtenni, de most megtehetjük, mert ugyan ennek a pontnak van gyorsulása, de a gyorsulásvektor merőleges a felületre, és így átmegy a test tömegközéppontján (lásd Szvetnik Endre ,,Forgási egyenlet tetszőleges tengelyre'' c. cikkét a KöMaL 1993. májusi számában http://db.komal.hu/KomalHU/cikk.phtml?id=199387). Erre a pontra vonatkoztatva csak a nehézségi erőnek van forgatónyomatéka:
\(\displaystyle \theta_C\beta_\varphi=-mgr\sin\phi,\)
ahol \(\displaystyle \theta_C=\theta+mr^2\) (\(\displaystyle \theta\) az előző megoldással egyezően a hengernek a szimmetriatengelyére vonatkozó tehetetlenségi nyomatéka). Ezt behelyettesítve, felhasználva a szöggyorsulások közötti összefüggést, valamint a kis \(\displaystyle \phi\) esetén érvényes \(\displaystyle \sin\phi\cong\phi\) közelítést:
$$\begin{align*} (\theta+mr^2)\frac{R-r}{r}\beta_\phi &=-mgr\phi,\\ \beta_\phi &=-\frac{g}{(1+\frac{\theta}{mr^2})(R-r)}\phi, \end{align*}$$amelyből az előző megoldással egyező módon következik a rezgés körfrekvenciája és periódusideje.
III. megoldás. Számítsuk ki – az I. megoldás jelöléseit használva – a görgő gravitációs helyzeti energiáját és a mozgási energiáját az ábrán látható helyzetben.
A helyzeti energia (annak nullpontját a henger legmélyebb helyzetéhez választva):
\(\displaystyle E_\mathrm{h}=mg(R-r)(1-\cos\phi).\)
Kis kitéréseknél \(\displaystyle \cos\phi=1-2\sin^2(\phi/2)\approx 1-\frac{\phi^2}{2}\), így
\(\displaystyle E_\mathrm{h}=mg(R-r)\frac{\phi^2}{2}.\)
Ez az energia éppen olyan, mint egy
\(\displaystyle D=mg(R-r)\)
rugóállandójú rugó rugalmas energiája \(\displaystyle \phi\) megnyújtás esetén.
Amikor a \(\displaystyle \phi\) szög változási sebessége \(\displaystyle \omega_\phi\), akkor a tapadási kényszerfeltétel miatt a görgő szögsebessége
\(\displaystyle \omega_\varphi=\frac{R-r}{r}\omega_\phi,\)
és így a mozgási energiája a tömegközéppont mozgásához tartozó energia és a forgási energia összege, vagyis (kis kitérések esetén)
\(\displaystyle E_\mathrm{m}=\frac{1}{2}m(R-r)^2\omega_\phi^2+\frac{1}{2}\,\frac{mr^2}2\omega_\varphi^2=\frac{3}{4}m(R-r)^2\omega_\phi^2.\)
Ez a kifejezés ugyanolyan, mint egy
\(\displaystyle M=\frac{3}{2}m(R-r)^2\)
tömegű, \(\displaystyle v=\omega_\phi\) sebességgel mozgó pontszerű test mozgási energiája.
A görgő mozgásának periódusideje a rugó végén mozgó tömegponttal való hasonlóság miatt
\(\displaystyle T=2\pi\sqrt{\frac{M}{D}}=2\pi\sqrt{\frac{3}{2}\frac{R-r}{g}}.\)
Statistics:
38 students sent a solution. 5 points: Csiszár András, Csóka Péter, Czirják Márton Pál, Erős Fanni, Hegedüs Márk, Masa Barnabás, Szabó Donát, Žigo Boglárka. 4 points: Csapó András, Kiss 131 Adorján Timon, Sütő Áron. 3 points: 7 students. 2 points: 9 students. 1 point: 8 students. Not shown because of missing birth date or parental permission: 1 solutions.
Problems in Physics of KöMaL, March 2024
