 Problem P. 5561. (March 2024)
Problem P. 5561. (March 2024)
P. 5561. On a stretched string of length \(\displaystyle 2L\), fixed at both ends, with mass \(\displaystyle \mu\) per unit length, the speed of transverse waves is \(\displaystyle c\).
\(\displaystyle a)\) Give the possible frequencies of the eigenvibrations of the string in units \(\displaystyle c/L\).
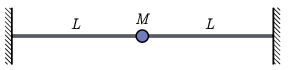
\(\displaystyle b)\) A point-like body of mass \(\displaystyle M=2\mu L\) is fixed at the centre of the string, as shown in the figure. Write an equation for the possible frequencies of the eigenvibrations of the string and calculate the numerical value of the lowest 3 frequencies in units \(\displaystyle c/L\). The effect of gravity is negligible.
Hint: It can be shown that the forms of the waves can be described by even or odd functions with respect to the centre.
(6 pont)
Deadline expired on April 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) A húron állóhullámok alakulnak ki, melyek lehetséges \(\displaystyle \lambda_n\) hullámhosszait a rögzített végek miatt a következő feltétel határozza meg:
\(\displaystyle n\frac{\lambda_n}{2}=2L,\)
ebből \(\displaystyle \lambda_n=4L/n\), ahol \(\displaystyle n=1,2,\ldots\) az alap- és felharmonikusoknak megfelelő pozitív egész számok. A megfelelő frekvenciák a fázissebesség segítségével így írhatók:
\(\displaystyle f_n=\frac{c}{\lambda_n}=\frac{n}{4}\frac{c}{L}.\)
\(\displaystyle b)\) Mivel most is sajátrezgéseket keresünk (azaz olyan mozgásformát, melyben a húr minden pontja és az \(\displaystyle M\) tömegű test is azonos frekvenciával, azonos vagy ellentétes fázisban mozog), a húr két felén egyforma hullámhosszú állóhullám fog kialakulni. Két lehetőség van: a húr két fele vagy azonos fázisban rezeg (ez a középpontra nézve páros függvénnyel írható le) vagy ellentétes fázisban (páratlan függvény). Utóbbi esetben a húr közepének (és így az \(\displaystyle M\) tömegű testnek) a kitérése nulla, ezért ekkor a hullámhosszt meghatározó egyenlet:
\(\displaystyle n\frac{\lambda_n}{2}=L,\qquad\textrm{ahonnan}\qquad f_n=\frac{n}{2}\frac{c}{L}.\)
Itt továbbra is \(\displaystyle n=1,2,\ldots\) egész számok.
A tengelyesen szimmetrikus (páros) megoldásokhoz tartozó sajátfrekvenciák meghatározása egy kicsit nehezebb, melynek oka, hogy a húr közepén a peremfeltétel nem olyan egyszerű, mint rögzített vagy szabad végpont esetében. Válasszunk olyan koordináta-rendszert, melynek origója a húr bal oldali rögzített végpontjában helyezkedik el (\(\displaystyle x=0\)), a pontszerű test vízszintes koordinátája pedig \(\displaystyle x=L\). A húr bal felén kialakuló transzverzális állóhullám
\(\displaystyle y(x,t)=A\sin(kx)\cos(\omega t)\)
alakban írható fel, hiszen az \(\displaystyle x=0\) helyen rögzített végpont kitérése minden időpillanatban szükségszerűen nulla. Ebben az egyenletben \(\displaystyle k=2\pi/\lambda\) a hullámszám és \(\displaystyle \omega=2\pi f\) a körfrekvencia. A húr gyorsulása az \(\displaystyle x=L\) helyen megegyezik az \(\displaystyle M\) tömegű test \(\displaystyle a\) gyorsulásával:
\(\displaystyle a=\left.\frac{\partial^2y}{\partial t^2}\right\vert_{x=L}=-A\omega^2\sin(kL)\cos(\omega t).\)
A pontszerű test rezgőmozgásának dinamikai feltételét a húrt feszítő \(\displaystyle F\) erő függőleges komponenséből származó eredő erő biztosítja:
\(\displaystyle -2F\sin\alpha=Ma,\)
ahol \(\displaystyle \sin\alpha\) kis kitérések esetén közelíthető a húr érintőjének meredekségével az \(\displaystyle x=L\) helyen:
\(\displaystyle \sin \alpha\approx\tg \alpha =\left.\frac{\partial y}{\partial x}\right\vert_{x=L}=Ak\cos(kL)\cos(\omega t).\)
Az utóbbi három összefüggés felhasználásával a következőt kapjuk:
\(\displaystyle 2FAk\cos(kL)=MA\omega^2\sin(kL).\)
Használjuk fel a húrt feszítő erő és a fázissebesség között fennálló \(\displaystyle c=\sqrt{F/\mu}\) összefüggést, valamint a feladatban megadott \(\displaystyle M=2\mu L\) tömegértéket! Egyszerűsítés és rendezés után kapjuk a
\(\displaystyle c^2k=L\omega^2\tg(kL)\)
egyenletet, ami az \(\displaystyle \omega=ck\) formula segítségével elegáns alakba írható:
\(\displaystyle kL\tg(kL)=1.\)
Ennek a transzcendens egyenletnek a gyökei határozzák meg a lehetséges \(\displaystyle k\) hullámszámokat és az annak megfelelő sajátfrekvenciákat. A gyökök numerikusan (pl. zsebszámológéppel) vagy számítógéppel kereshetők meg, az első három pozitív megoldás:
\(\displaystyle kL=0{,}860\quad 3{,}426\quad 6{,}437\quad\ldots\)
A megfelelő frekvenciák a hullámszám lehetséges értékeinek ismeretében így számolhatók:
\(\displaystyle f=\frac{\omega}{2\pi}=\frac{ck}{2\pi}.\)
A tengelyesen szimmetrikus hullámformákhoz tartozó sajátfrekvenciák tehát:
\(\displaystyle f=0{,}136\frac{c}{L},\quad 0{,}545 \frac{c}{L},\quad 1{,}024\frac{c}{L}\,\quad\ldots\)
A feladat a három legalacsonyabb frekvenciát kérdezte, ezek közül kettő a páros megoldásokhoz, egy pedig a páratlanhoz tartozik:
\(\displaystyle f=0{,}136\frac{c}{L},\quad 0{,}500\frac{c}{L},\quad 0{,}545\frac{c}{L}.\)
Statistics:
3 students sent a solution. 2 points: 2 students. 1 point: 1 student.
Problems in Physics of KöMaL, March 2024
