 Problem P. 5581. (September 2024)
Problem P. 5581. (September 2024)
P. 5581. Two rings of different radii are made from thin, flexible steel strips. Each ring slides on a horizontal tabletop, and there is a retarding (viscous-type) force exerted on each, which is proportional to the radius of the ring and to the instantaneous speed of the ring. If the smaller ring is started at \(\displaystyle v_0\), it travels a distance of \(\displaystyle L_0\) until it stops. Push one of the rings so that it collides with the initially stationary other ring such that its velocity before the collision is \(\displaystyle v\). What is the distance between the rings when both stop, if the collision is elastic and
\(\displaystyle a)\) along a straight line,
\(\displaystyle b)\) oblique?
The rings do not rotate either before or after the collisions, and their size is negligibly small with respect to the distances they travel after the collisions.
(5 pont)
Deadline expired on October 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Egyenes ütközés esetén a karikák középpontja egy egyenes mentén mozog, emiatt az elmozdulás, sebesség és gyorsulás (előjeles) skalár mennyiségekkel adható meg. Nem egyenes ütközésnél az elmozdulás, a sebesség és a gyorsulás (síkbeli) vektorokkal írható le. Ez utóbbi az általánosabb eset, ami magában foglalja az egyenes ütközést is.
A karikák tömege arányos a méretükkel (sugarukkal), emiatt a fékezőerő így írható fel: \(\displaystyle \boldsymbol{F}=-km\boldsymbol{v}\), ahol \(\displaystyle k\) egy állandó. A Newton-féle mozgásegyenlet szerint
\(\displaystyle m\boldsymbol{a}=-km\boldsymbol{v},\)
vagyis
\(\displaystyle \boldsymbol{a}+k\boldsymbol{v}=0.\)
Mivel a gyorsulásvektor a sebességvektor időbeli változásának ütemével (idő szerinti deriváltjával) egyezik meg, a sebességvektor pedig az \(\displaystyle \boldsymbol{r}\) helyvektor változási ütemét adja meg, ha \(\displaystyle \boldsymbol{a}+k\boldsymbol{v}=0,\) akkor
| \(\displaystyle (1)\) | \(\displaystyle \boldsymbol{v}+k\boldsymbol{r}=\text{állandó vektor},\) |
hiszen a változásának üteme nulla. Ha valamelyik karika kezdetben az \(\displaystyle \boldsymbol{r}_0\) helyen \(\displaystyle \boldsymbol{v}_0\) sebességgel mozgott, és az \(\displaystyle r_1\) helyen áll meg, akkor az (1) megmaradási tétel szerint
\(\displaystyle \boldsymbol{v}_0+k\boldsymbol{r}_0=k\boldsymbol{r}_1,\)
vagyis az elmozdulásvektor az indulástól a megállásig:
\(\displaystyle \boldsymbol{L}_0=\boldsymbol{r}_1-\boldsymbol{r}_0=\frac{1}{k}\,\boldsymbol{v}_0.\)
A megadott feltétel szerint \(\displaystyle L_0=v_0/k,\) vagyis \(\displaystyle k=v_0/L_0.\) Ennek megfelelően a karika elmozdulásvektora a \(\displaystyle \boldsymbol{v}\) kezdősebességű indulástól a megállásig
\(\displaystyle \boldsymbol{L}=\frac{L_0}{v_0}\boldsymbol{v}.\)
Megjegyzés. A karika
\(\displaystyle \frac{\mathrm{d}v(t)}{\mathrm{d}t}=-kv(t)\)
mozgásegyenlete a radioaktív bomlások egyenletével azonos alakú, és a megoldása:
\(\displaystyle v(t)=v_0\mathrm{e}^{-kt}.\)
Látszik, hogy véges hosszúságú idő alatt a sebesség nem válik nullává, tehát a karika elvben sohasem áll meg. Másrészt igaz, hogy néhányszor (mondjuk 5-ször) \(\displaystyle 1/k\) idő alatt a sebesség a kezdeti értéknek olyan kicsiny részére csökken, hogy gyakorlatilag nullának tekinthető.
a) Legyen a kezdetben álló karika tömege \(\displaystyle M\), a nekiütköző karikáé \(\displaystyle m\). Az ütközés utáni sebességeket jelölje \(\displaystyle \boldsymbol{U}\) és \(\displaystyle \boldsymbol{u}\) (1. ábra).

1. ábra
Egyenes ütközés esetén a sebességvektorok helyett elegendő azok (előjeles) nagyságával, \(\displaystyle U\)-val és \(\displaystyle u\)-val számolni. Nyilván \(\displaystyle U>u\), és a két karika távolsága a megállásukkor
\(\displaystyle L=\frac{L_0}{v_0}U-\frac{L_0}{v_0}u=\frac{L_0}{v_0}(U-u).\)
Az impulzus- és az energiamegmaradás törvénye szerint
\(\displaystyle mv=mu+MU,\qquad\text{illetve}\qquad\frac{1}{2}mv^2=\frac{1}{2}mu^2+\frac{1}{2}MU^2.\)
Ez a két összefüggés egyértelműen meghatározza az ütközés utáni sebességeket:
\(\displaystyle u=\frac{m-M}{m+M}v,\qquad U=\frac{2m}{m+M}v,\)
tehát
\(\displaystyle U-u=\frac{2m}{m+M}v-\frac{m-M}{m+M}v=v,\)
és a keresett távolság:
\(\displaystyle L=\frac{v}{v_0}L_0.\)
Érdekes, hogy ez a távolság a karikák méretétől (tömegétől) függetlenül minden esetben ugyanakkora.
b) Ha az ütközés nem egyenes, a megmaradási törvények nem határozzák meg egyértelműen a karikák ütközés utáni sebességét. Ennek ellenére igaz, hogy
\(\displaystyle \vert\boldsymbol{U}-\boldsymbol{u}\vert=v,\)
és emiatt a karikák elmozdulásvektorai \(\displaystyle \boldsymbol{R}=\frac{L_0}{v_0}\boldsymbol{U}\) és \(\displaystyle \boldsymbol{r}=\frac{L_0}{v_0}\boldsymbol{u}\), a végső távolságuk pedig
\(\displaystyle L=\vert\boldsymbol{R}-\boldsymbol{r}\vert=\vert\boldsymbol{U}-\boldsymbol{u}\vert\,\frac{L_0}{v_0}=\frac{v}{v_0}L_0.\)
Az ütközés utáni relatív sebesség nagyságáról háromféle módszerrel is belátjuk, hogy az \(\displaystyle v\)-vel egyezik meg.
1. módszer: Megmaradási törvények alkalmazása. Az impulzus- és az energiamegmaradás törvénye szerint
\(\displaystyle m\boldsymbol{v}=m\boldsymbol{u}+M\boldsymbol{U},\qquad\text{illetve}\qquad\frac{1}{2}mv^2=\frac{1}{2}mu^2+\frac{1}{2}MU^2,\)
vagyis
| \(\displaystyle (2)\) | \(\displaystyle \boldsymbol{v}=\boldsymbol{u}+\frac{M}{m}\boldsymbol{U},\) |
és
| \(\displaystyle (3)\) | \(\displaystyle v^2=u^2+\frac{M}{m}U^2.\) |
A (2) egyenlet négyzetét (önmagával való skaláris szorzatát) (3)-mal összevetve kapjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle 2\boldsymbol{u}\cdot\boldsymbol{U}=\left(1-\frac{M}{m}\right)\,U^2.\) |
Számítsuk ki most az \(\displaystyle \boldsymbol{U}-\boldsymbol{u}\) vektor önmagával való skalárszorzatát, vagyis a relatív sebesség négyzetét:
\(\displaystyle \left(\boldsymbol{U}-\boldsymbol{u}\right)^2=U^2+u^2-2\boldsymbol{u}\cdot\boldsymbol{U}.\)
Felhasználva a (4), majd a (3) összefüggést, megkapjuk, hogy
\(\displaystyle \left(\boldsymbol{U}-\boldsymbol{u}\right)^2=U^2+u^2-\left(1-\frac{M}{m}\right)\,U^2=u^2+\frac{M}{m}U^2=v^2,\)
tehát \(\displaystyle \vert\boldsymbol{U}-\boldsymbol{u}\vert=v\).
2. módszer: Tömegközépponti rendszer előnyei. Ha két test relatív sebessége valamely vonatkoztatási rendszerben \(\displaystyle \Delta\boldsymbol{v}\), akkor bármely másik, az eredetihez képest mozgó koordináta-rendszerben az egymáshoz viszonyított sebesség ugyanekkora \(\displaystyle \Delta\boldsymbol{v}\). A ,,mozgó'' rendszerre való áttéréskor mindegyik sebességhez ugyanaz a vektor (a vonatkoztatási rendszerek egymáshoz viszonyított sebessége) adódik hozzá, ez tehát a sebességvektorok különbségéből kiesik. (Fizikus szaknyelven szólva: a relatív sebesség Galilei-invariáns mennyiség.)
Két test tömegközépponti (TKP) rendszerében a testek impulzusa (lendülete) \(\displaystyle \boldsymbol{p}\) és \(\displaystyle -\boldsymbol{p}\). A testek rugalmas ütközésekor az impulzusok a TKP-i rendszerben \(\displaystyle \boldsymbol{p}'\) és \(\displaystyle -\boldsymbol{p}'\)-re változnak. Amennyiben az ütközés rugalmas, a \(\displaystyle p^2\)-tel, illetve \(\displaystyle p'^2\)-tel arányos mozgási energia megmaradó mennyiség, fennáll tehát \(\displaystyle \vert\boldsymbol{p}\vert=\vert\boldsymbol{p}'\vert\). A testek sebessége a TKP-i rendszerben egymással ellentétes irányú. A sebességkülönbség is arányos \(\displaystyle p\)-vel, illetve \(\displaystyle p'\)-vel. Mivel az ütközésnél az impulzusok nagysága nem változik, a sebességkülönbségek nagysága is változatlan marad (2. ábra).
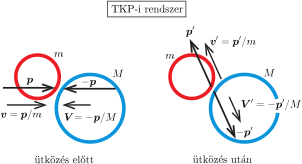
2. ábra
Az eredeti (laboratóriumi) rendszerben a sebességkülönbség nagysága \(\displaystyle v\). A Galilei-invariancia miatt ugyanekkora kell, hogy legyen az ütközés utáni sebességkülönbség is, vagyis \(\displaystyle \vert\boldsymbol{U}-\boldsymbol{u}\vert=v\).
3. módszer: Síkbeli vektorok komplex számokkal. A KöMaL 2024. évi áprilisi számában megjelent Komplex számok a fizikában I. cikk szerint bármely síkbeli \(\displaystyle \boldsymbol{w}=(w_x,w_y)\) vektornak kölcsönösen egyértelműen megfeleltethető egy komplex szám: \(\displaystyle w^*=w_x+iw_y\). (A \(\displaystyle ^*\) azt jelzi, hogy komplex számról van szó, amely különbözik a \(\displaystyle \boldsymbol{w}\) vektor \(\displaystyle w\)-vel jelölt hosszától.)
A ,,komplex vektorokkal'' kényelmesen tárgyalhatók bizonyos fizikai problémák, pl. síkban mozgó testek ütközése. Az idézett cikkben leírtak szerint (a jelöléseket a jelen esethez igazítva), ha egy \(\displaystyle M\) tömegű, álló karikának egy másik, \(\displaystyle m\) tömegű karika \(\displaystyle w^*=v\) sebességgel nekiütközik, akkor a két test sebessége az ütközés után
\(\displaystyle u^*=\left(\frac{m}{M+m}+\frac{M}{M+m}\mathrm{e}^{2i\alpha}\right)v\qquad\text{és}\qquad U^*=\frac{m}{M+m}\left(1-\mathrm{e}^{2i\alpha}\right)v,\)
ahol \(\displaystyle \alpha\) az ütközés ,,ferdeségére'' jellemző szög. A két test relatív sebessége
\(\displaystyle u^*-U^*=\mathrm{e}^{2i\alpha}\,v,\)
melynek nagysága (a komplex szám abszolút értéke):
\(\displaystyle \vert\boldsymbol{u}-\boldsymbol{U}\vert=\vert u^*-U^*\vert=\left|\mathrm{e}^{2i\alpha}\right|v=v.\)
Statistics:
18 students sent a solution. 5 points: Beke Márton Csaba, Simon János Dániel, Tóth Kolos Barnabás, Ujpál Bálint, Ujvári Sarolta, Zólomy Csanád Zsolt. 4 points: Gyenes Károly, Kiss 131 Adorján Timon, Kovács Tamás, Sütő Áron. 3 points: 2 students. 2 points: 1 student. Unfair, not evaluated: 1 solutions.
Problems in Physics of KöMaL, September 2024
