 Problem P. 5582. (September 2024)
Problem P. 5582. (September 2024)
P. 5582. Using the data from the Cassini spacecraft, a spectacular video (https://www.flickr.com/photos/kevinmgill/44583965185/) has been produced, which shows how Jupiter's moon Europa ``overtook'' the moon Io. This appears to contradict Kepler's laws, since Io, which is closer to Jupiter, has a higher orbital speed than the more distant moon Europa. The resolution to the paradox is the fact that the Cassini probe was also moving when the image was taken. At most how far away from Jupiter can a spacecraft orbiting the planet be, and in what direction should it move, to make such a strange ``role reversal''? Consider the moons and the spacecraft orbiting in nearly the same planes along circular paths.
(5 pont)
Deadline expired on October 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Belátjuk, hogy a leírt jelenség csak akkor jöhet létre, ha az űrszonda a holdakkal ellentétes irányba kering a Jupiter körül.
Megjegyzés. A Cassini űrszonda ténylegesen nem keringett a Jupiter körül, hanem elhaladt az óriásbolygó mellett, és annak gravitációs lendítését (is) kihasználva jutott el a Szaturnusz közelébe. Emiatt szerepel a feladat szövegében ,,egy, a bolygó körül keringő űrszonda'', ami tehát nem a Cassini.
Jelöljük az Io keringési sugarát (a Jupiter középpontjától mért átlagos távolságot) \(\displaystyle r_1\)-gyel, az Europa pályasugarát \(\displaystyle r_2\)-vel, az űrszondáét pedig \(\displaystyle R\)-rel. A megfelelő keringési sebességek legyenek \(\displaystyle v_1,\,v_2\) és \(\displaystyle V\).
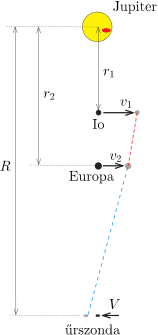
Az ábráról leolvasható, hogy a 2-es jelzésű Europa akkor tudja – látszólag – megelőzni az 1-es jelzésű Io holdat, ha egy kicsiny \(\displaystyle t\) idő alatt teljesül, hogy
| \(\displaystyle (1)\) | \(\displaystyle \frac{v_2t+Vt}{R-r_2} >\frac{v_1t+Vt}{R-r_1}.\) |
Használjuk még ki, hogy Kepler III. törvénye szerint
\(\displaystyle T^2\sim \frac{r^2}{v^2}\sim r^3,\qquad \text{vagyis}\qquad v \sim \frac{1}{\sqrt{r}}.\)
Eszerint (1) így is felírható:
\(\displaystyle \frac{\frac{1}{\sqrt{r_2}}+\frac{1}{\sqrt{R}}}{R-r_2}>\frac{\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{R}}}{R-r_1},\)
azaz
\(\displaystyle \frac{1}{\sqrt{Rr_2}\left(\sqrt{R}-\sqrt{r_2}\right)}>\frac{1}{\sqrt{Rr_1}\left(\sqrt{R}-\sqrt{r_1}\right)},\)
tehát
\(\displaystyle \sqrt{r_1}\left(\sqrt{R}-\sqrt{r_1}\right)>\sqrt{r_2}\left(\sqrt{R}-\sqrt{r_2}\right),\)
| \(\displaystyle (2)\) | \(\displaystyle \sqrt{R} \left(\sqrt{r_2}-\sqrt{r_1}\right)<r_2-r_1,\) |
és így
\(\displaystyle \sqrt{R}<\frac{r_2-r_1}{\sqrt{r_2}-\sqrt{r_1}}=\sqrt{r_1}+\sqrt{r_2},\)
azaz
| \(\displaystyle (3)\) | \(\displaystyle R<\Bigl(\sqrt{r_1}+\sqrt{r_2}\Bigr)^2.\) |
Megjegyzés. Ha az űrszonda a holdakkal megegyező irányba kering, akkor (1)-ben \(\displaystyle V\) előjele negatívra változik, és a fentiekkel megegyező lépések után (2) helyett a
| \(\displaystyle (2^*)\) | \(\displaystyle \sqrt{R} \left(\sqrt{r_1}-\sqrt{r_2}\right)>r_2-r_1 \) |
feltételt kapjuk. Ez azonban semekkora \(\displaystyle R\)-re nem teljesül, hiszen \(\displaystyle r_1<r_2\) miatt a bal oldal negatív, a jobb oldal pedig pozitív.
Táblázati adatok szerint \(\displaystyle r_1=421{,}8\cdot 10^3\,\mathrm{km}\) és \(\displaystyle r_2=671{,}8\cdot 10^3\,\mathrm{km}\), innen (3)-ból kapjuk: az űrszonda pályasugara legfeljebb 2,16 millió km lehet.
Statistics:
16 students sent a solution. 5 points: Bélteki Teó, Kovács Tamás, Tóthpál-Demeter Márk, Ujpál Bálint, Zólomy Csanád Zsolt. 4 points: Horvath Benedek. 3 points: 4 students. 2 points: 2 students. 1 point: 2 students.
Problems in Physics of KöMaL, September 2024
