 Problem P. 5592. (October 2024)
Problem P. 5592. (October 2024)
P. 5592. The suspension points of a weightless inextensible rope are located at a horizontal distance of \(\displaystyle L\) and a vertical distance of \(\displaystyle H\) from each other as shown in the figure. On a cold winter day, snow of density \(\displaystyle \varrho\) accumulated on the rope in width of \(\displaystyle d\). The height of the snow layer varies linearly as a function of the horizontal coordinate, between zero and \(\displaystyle h_\textrm{max}\). At the equilibrium position, the tangent of the rope at its right-hand end is exactly horizontal. Determine the minimum and maximum tension in the rope.

(5 pont)
Deadline expired on November 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A megoldás első lépéseként gondoljuk végig, hogy a kötél mely keresztmetszetében lép fel a minimális, illetve maximális húzóerő! Tudjuk, hogy erő csak a kötél irányában ébredhet, ebből következik, hogy a jobb oldali végpontban fellépő húzóerő éppen vízszintes. Mivel a felhalmozódott hó tömegéből származó erőhatás függőleges irányú, és más külső erő nem hat a rendszerre, a kötélben keletkező húzóerő vízszintes komponense minden keresztmetszetben megegyezik. Az előzőekből egyértelműen következik, hogy a minimális kötélerő éppen a jobb oldali végpontban lép fel, míg a maximális érték a bal oldali végpontban keletkezik (hiszen a kötél érintőjének meredeksége, és így a függőleges irányú erőkomponens itt a legnagyobb).
A fentiek alapján rajzoljuk fel a kötélre ható erőket, ezt szemlélteti az ábra. Jelölje a kötél bal oldali végpontját \(\displaystyle A\), jobb oldali végpontját pedig \(\displaystyle B\)! Ekkor az \(\displaystyle A\) pontban fellépő húzóerő komponensei legyenek \(\displaystyle K_{A,y}\) és \(\displaystyle K_{A,x}\), a \(\displaystyle B\) pontban keletkező húzóerőt pedig jelölje \(\displaystyle K_B\). A felhalmozódott hó hatását egy, a kötél vízszintes vetülete mentén lineárisan változó erőként kezelhetjük, melynek \(\displaystyle f=\tfrac{\Delta F}{\Delta x}\) ,,intenzitása'' a kötél bal oldali végpontján zérus, jobb oldalán pedig
\(\displaystyle f_\mathrm{max}=\varrho gdh_\mathrm{max}.\)
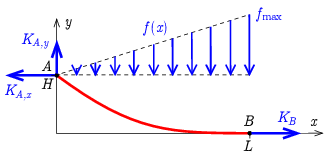
A továbbiakban vizsgáljuk a kötél, mint kiterjedt test egyensúlyát! Ekkor tudjuk, hogy a kötélre ható erők, valamint forgatónyomatékok eredőjének bármely pontra nézve zérusnak kell lennie. Felírva vízszintes irányban az erők eredőjére vonatkozó feltételt:
\(\displaystyle K_{A,x}=K_B,\)
továbbá függőleges irányban:
\(\displaystyle K_{A,y}=\frac{f_\mathrm{max}L}{2}=\frac{\varrho gdh_\mathrm{max}L}{2}.\)
Írjuk fel a testre ható forgatónyomatékokat az \(\displaystyle A\) pontra:
\(\displaystyle K_BH=\frac{f_\mathrm{max}L}{2}\cdot\frac{2}{3}L=\frac{f_\mathrm{max}L^2}{3},\)
beírva \(\displaystyle f_\mathrm{max}\) kifejezését, majd \(\displaystyle K_B\)-re rendezve:
\(\displaystyle K_B=\frac{\varrho gdh_\mathrm{max}L^2}{3H}.\)
Azaz a kötélben keletkező minimális húzóerő:
\(\displaystyle K_\mathrm{min}=K_B=\frac{\varrho gdh_\mathrm{max}L^2}{3H},\)
a fellépő maximális erő pedig a Pitagorasz-tételt felhasználva:
\(\displaystyle K_\mathrm{max}=\sqrt{K^2_{A,x}+K^2_{A,y}}=\frac{\varrho gdh_\mathrm{max}L}{6H}\sqrt{9H^2+4L^2}.\)
Statistics:
15 students sent a solution. 5 points: Beke Márton Csaba, Erdélyi Dominik, Sütő Áron, Tóth Kolos Barnabás, Tóthpál-Demeter Márk, Ujpál Bálint. 4 points: Elekes Panni, Kiss 131 Adorján Timon, Kovács Tamás, Tóth Hanga Katalin. 3 points: 1 student. 2 points: 4 students.
Problems in Physics of KöMaL, October 2024
