 Problem P. 5615. (December 2024)
Problem P. 5615. (December 2024)
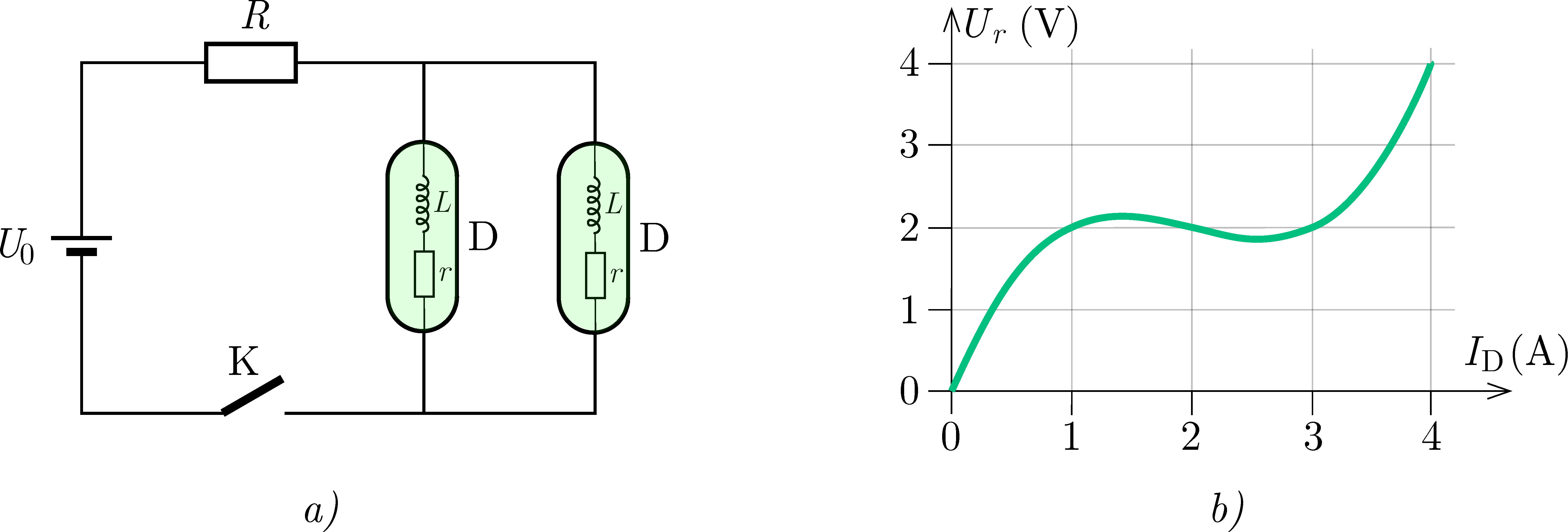
P. 5615. Using an ideal battery with an electromotive force of \(\displaystyle U_0=4~\mathrm{V}\), a load with a resistance of \(\displaystyle R=0.5~\Omega\), a switch and two düristors (D), we construct the circuit shown in figure a. A düristor is a circuit element consisting of an ideal coil with inductance \(\displaystyle L=1~\mathrm{H}\) and a non-linear resistor of resistance \(\displaystyle r\), which are connected in series. The \(\displaystyle U_r(I_\mathrm{D})\) characteristics of the resistor is shown in figure b. a) In the stationary (that is, constant in time) case, what are the currents in the sub-branches?
Hint: See problem P. 5604. and its solution in the workbook.
b) At the moment \(\displaystyle t=0\) we turn on the switch. Sketch the currents flowing through the düristors as a function of time. What will these currents be after a long time elapsed?
Hint: Suppose that during this time, due to symmetry, the same current flows through each düristor.
c) During the equilibrium state a small imbalance occurs: the current through one of the düristors decreases by a very small amount, and the current of the other increases by the same amount. Plot the currents of the two düristors as a function of time, after this imbalance occurs. What will the currents of each of the two düristors be after a long time elapsed? What can we say about the stability of the stationary solutions given in a)?
Hint: We can use that if the small imbalance is symmetric with respect to the first equilibrium state, then the sum of the currents through the two düristors remains constant.
(6 pont)
Deadline expired on January 15, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. a) A két párhuzamosan kapcsolt dürisztor teljes \(\displaystyle U(I)\) karakterisztikáját azokon a feszültségeken, amelyekhez csak egy lehetséges áramérték tartozik, a megadott karakterisztika vízszintesen kétszeresére nyújtásával kaphatjuk meg, a P. 5604. feladat megoldásához hasonlóan. Ahol több (két vagy három) lehetséges áramérték tartozik egy feszültséghez, ott ezek tetszőleges kombinációja (akár hat különböző érték) lehet az eredő áram, így ezen a tartományon a vízszintesen kétszeresére megnyújtott görbén kívül újabb ágak jelennek meg. Ezek jellegzetes pontjait grafikus összeadással szerkeszthetjük meg.
Megjegyzés. A szerkesztés négy különböző esetben az 1. ábrán látható (a jobb láthatóság miatt a rajz nagyított és függőleges irányban meg van nyújtva).
A legalsó (fekete) pontnál a feszültséghez csak egy áramérték tartozik, így a párhuzamosan kapcsolt dürisztorok karakterisztikáján csak egy pont keletkezik, amelynek áramértéke az eredeti karakterisztikán lévő áramérték kétszerese. Ezt a pontot megkapjuk a karakterisztika nyújtásával is.
A következő esetben a feszültség éppen a karakterisztika lokális minimumához tartozó érték, ezt két különböző áramértéknél veszi fel (kék pöttyök). A párhuzamos kapcsolás árama lehet mindkettő duplája (ezeket adja meg a teljes grafikon vízszintes irányú nyújtása), de lehet a két áramérték összege is (1+2). Ugyanígy járhatnánk el a karakterisztika lokális maximumánál is.
A harmadik eset a karakterisztika középpontjához tartozó feszültségérték: itt az eredeti karakterisztikán három lehetséges áramérték van (lila pöttyök). Ezekből bármely kettő összege lehet a párhuzamos kapcsolás árama. A nyújtással is megkapható 1+1, 2+2 és 3+3 pontokon kívül megkapjuk az 1+2, 1+3 és 2+3 pontokat is – de ezek közül az 1+3 egybeesik a 2+2 ponttal, így itt öt lehetséges érték van.
A negyedik (narancs) esetben nincs ilyen egybeesés, ott mind a hat áramérték különböző. De erre a szerkesztésre már a grafikon megrajzolásához nincs is szükség: ha a második eset szerkesztését megismételjük a lokális maximumnál is, akkor a harmadik eset pontjaival együtt már megkapjuk a ,,kis ág'' minden fontos pontját (elágazás, keresztezés, szélsőértékek), amely alapján már a teljes karakterisztika felvázolható.
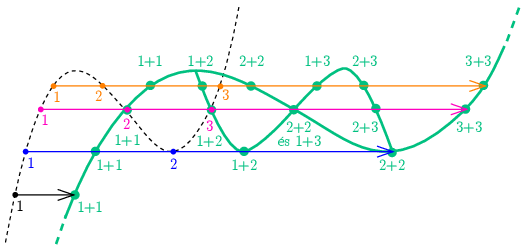
1. ábra
A végeredmény a 2. ábrán látható, amelybe már berajzoltuk a telep és az \(\displaystyle R\) ellenállás együttes \(\displaystyle U(I)\) karakterisztikáját is. A két görbe – esetünkben egyetlen – metszéspontja adja meg a párhuzamos kapcsolás stacionárius munkapontját: a dürisztorokon \(\displaystyle U_\mathrm{D}=2\,\mathrm{V}\) feszültség esik, és összesen \(\displaystyle I_{\Sigma\mathrm{D}}=4\,\mathrm{A}\) áram folyik. (Stacionárius állapotban a tekercsek feszültsége nulla, a dürisztor teljes feszültsége megegyezik a karakterisztikáról leolvashatóval.)
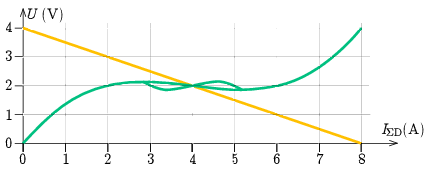
2. ábra
Visszatérve egyetlen dürisztor karakterisztikájára (3. ábra) látható, hogy ez kétféleképpen valósulhat meg: vagy mindkét dürisztoron \(\displaystyle I_\mathrm{D1}=I_\mathrm{D2}=2\,\mathrm{A}\) áram folyik, vagy pedig az egyiken \(\displaystyle I_\mathrm{D1}=1\,\mathrm{A}\) és a másikon \(\displaystyle I_\mathrm{D2}=3\,\mathrm{A}\).

3. ábra
b) Bekapcsoláskor mindenhol nulla áram folyik, a külső és a dürisztorokban lévő belső ellenálláson se esik feszültség, a teljes \(\displaystyle U_0=4\,\mathrm{V}\) telepfeszültség a dürisztorokban lévő tekercsekre esik. Mivel \(\displaystyle U_L=L\dot I_L=L\dot I_\mathrm{D}\), a tekercsek (és így a dürisztor) árama, valamint a külső ellenállás \(\displaystyle 2I_\mathrm{D}\) árama is nőni fog. Ezzel változik a külső és belső ellenállásokon a feszültség is: a külső ellenálláson lineárisan (\(\displaystyle U_R=2RI_\mathrm{D}\)), a belső ellenállásokon a megadott nemlineáris karakterisztika szerint. A tekercsekre így kisebb feszültség jut, az áram növekedése lassul, de folytatódik mindaddig, amíg a tekercsre eső feszültség pozitív, azaz a külső és belső ellenállásokon eső feszültség nem éri el a telep feszültségét. Szimmetrikus esetben ez az \(\displaystyle I_\mathrm{D}=2\,\mathrm{A}\) és \(\displaystyle U_\mathrm{D}=2\,\mathrm{V}\) állapotban következik be, amikor \(\displaystyle U_R=2RI_\mathrm{D}=2\,\mathrm{V}\) és \(\displaystyle U_\mathrm{D}+U_R=U_0=4\,\mathrm{V}\). Tehát hosszabb idő után a dürisztorok árama \(\displaystyle I_\mathrm{D1}=I_\mathrm{D2}=2\,\mathrm{A}\). Az áramok időfüggése a 4. ábrán látható. (A pontos görbealak és az időskála csak numerikus számítással kapható meg, de a görbe jellege a fenti gondolatmenet alapján felvázolható.)
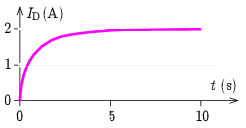
4. ábra
c) Jelöljük a b) részben kialakult egyensúlyi áramot és feszültséget \(\displaystyle I_\mathrm{D0}\)-lal és \(\displaystyle U_\mathrm{D0}\)-lal. A hirtelen kis zavar hatására \(\displaystyle I_\mathrm{D1}<I_\mathrm{D0}<I_\mathrm{D2}\), de eközben \(\displaystyle I_\mathrm{D1}+I_\mathrm{D2}=2I_\mathrm{D0}\), és így \(\displaystyle U_R\) és \(\displaystyle U_\mathrm{D}=U_0-U_R\) állandó marad. Az 1. dürisztorban lévő ellenálláson a kicsit lecsökkent áram miatt \(\displaystyle U_{r1}>U_\mathrm{D0}\) feszültség esik, az ebben lévő tekercs feszültsége így negatív lesz, és ennek a dürisztornak az árama emiatt tovább fog csökkenni. A 2. dürisztorban épp fordítva, a kicsit megnőtt áram miatt \(\displaystyle U_{r2}<U_\mathrm{D0}\), a tekercs feszültsége pozitívvá válik, és így ennek a dürisztornak az árama tovább fog nőni. (A karakterisztika középpontos szimmetriája miatt a változások ellentétes előjelűek, de azonos nagyságúak lesznek, így az összáram valóban nem változik.) Az áramok így kezdetben egyre gyorsulva változnak.
Amikor az egyes dürisztorokban lévő ellenállásokon eső feszültség eléri a lokális szélsőértékeket (\(\displaystyle I_\mathrm{D1}\approx 1{,}4\,\mathrm{A}\), illetve \(\displaystyle I_\mathrm{D2}\approx 2{,}6\,\mathrm{A}\)), akkor a feszültségek változási iránya megfordul, a tekercseken eső feszültségek előjele megmarad, de nagyságuk csökkenni kezd, és így az áramok egyre lassabban változnak. A folyamat akkor ér véget, amikor \(\displaystyle I_\mathrm{D1}=1\,\mathrm{A}\) és \(\displaystyle I_\mathrm{D2}=3\,\mathrm{A}\) lesz. Az áramok időfüggése az 5. ábrán látható. (A pontos görbealak és az időskála függ a zavar időpontjától és nagyságától, most is csak numerikus számítással kapható meg. A görbe jellege a megfontolások alapján ismét felvázolható.)
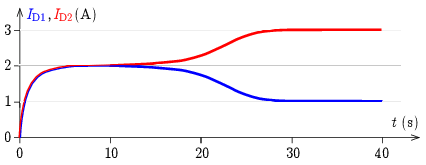
5. ábra
Láthattuk, hogy az azonos áramú egyensúly instabil, hiszen egy kis zavar hatására egyre gyorsulva távolodtak attól az értéktől az áramok. A rendszer az árammentes állapotból először mégis oda tart, mert ez az állapot a szimmetrikus tengely mentén stabil, csak az aszimmetrikus irányban instabil – mint egy nyeregfelület (6. ábra).
Ugyanakkor az aszimmetrikus állapot stabil, amit a következőképp láthatunk be: ha pl. \(\displaystyle I_\mathrm{D1}\) kicsit megnő, akkor az 1. dürisztor belső ellenállásán is megnő az áram, a tekercsen negatív feszültség lesz, ami az áramot csökkenti, visszaviszi az egyensúlyi értékre. Ellentétes irányú változásnál (és a másik dürisztoron is) hasonlóan negatív visszacsatolás alakul ki, ami stabilitást eredményez.

6. ábra
Megjegyzések. 1. A tényleges görbék numerikus módszerekkel könnyen megrajzolhatók. (Erről lásd lapunk novemberi számában Csóka Péter és Seprődi Barnabás: Fizika problémák megoldása numerikus módszerrel című cikkét.) Ehhez a grafikusan megadott karakterisztikára ez a harmadfokú polinom illeszthető (\(\displaystyle I_\mathrm{D}\) amperben, \(\displaystyle U_r\) voltban):
\(\displaystyle U_r=\frac{1}{3}I_\mathrm{D}^3-2I_\mathrm{D}^2+\frac{11}{3}I_\mathrm{D}.\)
A numerikus megoldáshoz a következő összefüggéseket írhatjuk fel:
$$\begin{align*} \Delta I_\mathrm{D1}&=\frac{1}{L}\left[U_0-R(I_\mathrm{D1}+I_\mathrm{D2})-\left(\frac{1}{3}I_\mathrm{D1}^3-2I_\mathrm{D1}^2+\frac{11}{3}I_\mathrm{D1}\right)\right]\Delta t,\\ \Delta I_\mathrm{D2}&=\frac{1}{L}\left[U_0-R(I_\mathrm{D1}+I_\mathrm{D2})-\left(\frac{1}{3}I_\mathrm{D2}^3-2I_\mathrm{D2}^2+\frac{11}{3}I_\mathrm{D2}\right)\right]\Delta t,\\ I_\mathrm{D1}(0)&=0,\\ I_\mathrm{D2}(0)&=0. \end{align*}$$A második szakasz időbeli lefutása függ a kis zavar nagyságától (minél nagyobb a zavar, annál gyorsabban történik). Az 5. ábrán látható grafikon \(\displaystyle \Delta t=0{,}1\,\mathrm{s}\) lépéssel, és egy \(\displaystyle t=10\,\mathrm{s}\) időpillanatban alkalmazott \(\displaystyle \Delta I_\mathrm{D}=\pm 0{,}01\,\mathrm{A}\) nagyságú zavarral készült.
2. Ha a rendszerbe beépítünk egy kicsiny véletlen zajt (és az nem túl nagy), a folyamat első része meglepő módon ugyanúgy végbemegy, a rendszer először (jó közelítéssel) megállapodik az instabil egyensúlyban, majd (a véletlen zaj amplitúdójától – és a véletlentől – függő idő után) elkezd onnan távolodni, hogy aztán végleg (jó közelítéssel) megállapodjon a stabil állapotban. Természetesen ilyenkor véletlenszerűen egyik vagy másik dürisztor árama csökken, illetve nő.
Statistics:
7 students sent a solution. 6 points: Fajszi Karsa. 5 points: Beke Márton Csaba, Erdélyi Dominik. 4 points: 1 student. 3 points: 1 student. 2 points: 2 students.
Problems in Physics of KöMaL, December 2024
