 Problem P. 5618. (January 2025)
Problem P. 5618. (January 2025)
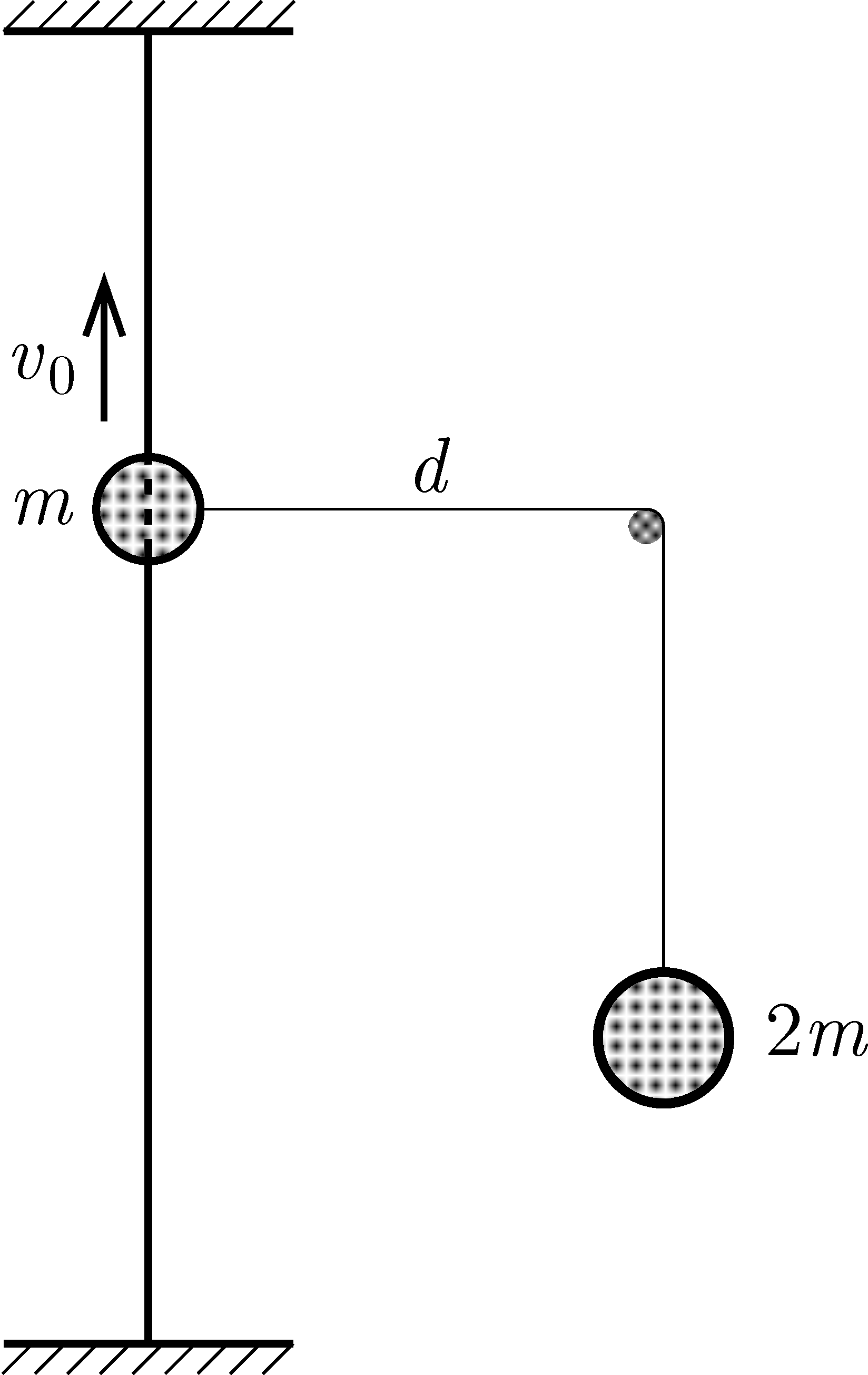
P. 5618. A bead with weight \(\displaystyle m\) was strung on a long enough fixed, taut, vertical wire to which a piece of yarn was attached. The yarn was laid over a horizontal rod as shown in the figure, and a small weight of mass \(\displaystyle 2m\) was attached to its vertically hanging end. The rod is at a distance \(\displaystyle d\) from the wire. When the yarn attached to the bead is in the horizontal position, the bead is given an initial upward velocity of \(\displaystyle v_0=\sqrt{2gd}\).
a) Let the distance of the top point of the path of the bead from its starting point be \(\displaystyle f\), and the distance of the bottom point of the path from the starting point be \(\displaystyle \ell\). What is the quotient \(\displaystyle \ell/f\)?
b) What is the tension in the yarn when the bead is at the topmost position and when the bead passes the initial position?
(Friction is negligible everywhere.)
(5 pont)
Deadline expired on February 17, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az a pályapont, amikor a fonálnak a gyöngyhöz rögzített szakasza vízszintes, nem egyensúlyi helyzet, de kitünteti, hogy a fonálon lógó test ilyenkor van a legmélyebben, és a sebessége ebben a helyzetben mindig nulla.
a) A szélső helyzetek pozícióit legegyszerűbben az energiamegmaradás törvényének segítségével számolhatjuk ki. A fentiek alapján a kiinduló helyzetben csak a gyöngy mozog, a kinetikus energiája pedig a feladatban megadott kezdősebességet behelyettesítve:
\(\displaystyle \frac{1}{2}mv_0^2=mgd.\)
Mérjük az elmozdulásokat a kiindulási helyzettől, ezek legyenek pozitívak, ha fölfelé mutatnak, és jelöljük a gyöngy és a lógó test magasságát a szélső helyzetben \(\displaystyle h_1\) illetve \(\displaystyle h_2\)-vel. Az energiamérleg szerint
\(\displaystyle mgd=mgh_1+2mgh_2.\)
A két magasság között a kötél nyújthatatlanságát kifejező egyenlet ad összefüggést. Ha a gyöngy pozíciója \(\displaystyle x_1\), a fonálon függő testé pedig \(\displaystyle x_2\), a Pitagorasz tétel szerint
\(\displaystyle x_1^2+d^2=\left(d+x_2\right)^2,\)
a szélső helyzetben tehát
\(\displaystyle \sqrt{h_1^2+d^2}-d=h_2.\)
Egyszerűsítések és a \(\displaystyle h_2\) kiküszöbölése a
\(\displaystyle 3d=h_1+2\sqrt{h_1^2+d^2}\)
egyenletre vezet, amelyből átrendezéssel és négyzetre emeléssel a
\(\displaystyle 3h_1^2+6dh_1-5d^2=0\)
másodfokú egyenlet kapható. Ennek a pozitív gyöke éppen \(\displaystyle f\), a negatív gyöke pedig az \(\displaystyle l\) mínusz egyszerese:
$$\begin{gather*} f=\left(\sqrt{\frac{8}{3}}-1\right)d,\\ l=\left(\sqrt{\frac{8}{3}}+1\right)d, \end{gather*}$$tehát
\(\displaystyle \frac{l}{f}=\frac{\sqrt{8}+\sqrt{3}}{\sqrt{8}-\sqrt{3}}=4{,}16.\)
b) A kötélerő meghatározásához a mozgásegyenleteket kell felírnunk! Jelöljük a gyöngy és a fonálon függő test gyorsulását \(\displaystyle a_1\) és \(\displaystyle a_2\)-vel, legyen \(\displaystyle K_1\) a fonalban ható erő, és \(\displaystyle \varphi\) a gyöngyhöz csatlakozó fonaldarab vízszintessel bezárt szöge a szélső helyzetben (\(\displaystyle \sin\varphi=f/\sqrt{f^2+d^2}\))! Ezekkel
$$\begin{gather*} ma_1=-mg-K_1\sin\varphi,\\ 2ma_2=-2mg+K_1. \end{gather*}$$A szélső helyzet közelében az egyes testek pozíciói (hiszen itt a sebesség zérus)
\(\displaystyle x_1=f+\frac{1}{2}a_1(\Delta t)^2,\)
illetve
\(\displaystyle x_2=h_2+\frac{1}{2}a_2(\Delta t)^2\)
alakúak, (ahol a gyorsulások értéke negatív, és a \(\displaystyle \Delta t\) az az idő, ami a szélső helyzet eléréséhez kell, vagy azóta eltelt). Ezeket az értékeket helyettesítve a kényszeregyenletbe, az összefüggést ad a két gyorsulás között:
\(\displaystyle \left(f+\frac{1}{2}a_1(\Delta t)^2\right)^2+d^2=\left(d+h_2+\frac{1}{2}a_2(\Delta t)^2\right)^2.\)
Ebből átrendezések után, a \(\displaystyle \Delta t\)-ben csak a vezető kvadratikus rendet megtartva az
\(\displaystyle f^2+d^2-\left(d+h_2\right)^2=\left((d+h_2)a_2-fa_1\right)(\Delta t)^2\)
egyenletet kapjuk. A baloldal \(\displaystyle f\) és \(\displaystyle h_2\) definíciója miatt nulla, tehát a jobb oldal is az, azaz
\(\displaystyle a_2=\frac{f}{d+h_2}a_1=a_1\sin\varphi.\)
A két mozgásegyenlettel együtt ez három ismeretlenre három egyenlet, aminek a megoldása a kötélerőre
\(\displaystyle K_1=\frac{2(1-\sin\varphi)}{1+2\sin^2\varphi}mg=0{,}592\,mg.\)
Abban a pillanatban, amikor a rendszer a kiinduló helyzeten áthalad, a kötél nem befolyásolja a gyöngy gyorsulását, mert a kötélerőnek nincs a drót irányába eső komponense. Ilyenkor tehát \(\displaystyle a_1=-g\) és a gyöngy mozgása jó közelítéssel az
\(\displaystyle x_1=\pm v_0(\delta t)-\frac{1}{2}g(\delta t)^2\)
formában adható meg, ahol a sebesség előjele utal arra, hogy milyen irányban halad át a rendszer az adott pozíción, és \(\displaystyle \delta t\) az ettől a pillanattól mért idő. A fonálon függő test a pályája legmélyebb pontja közelében van, mozgását az
\(\displaystyle x_2=\frac{1}{2}a_2(\delta t)^2\)
kifejezés adja meg. Itt, a kötélerőt \(\displaystyle K_2\)-vel jelölve,
\(\displaystyle 2ma_2=-2mg+K_2.\)
Ilyen \(\displaystyle x_1\) és \(\displaystyle x_2\) mellett a kötél nyújthatatlanságát a
\(\displaystyle d^2+\left(\pm v_0(\delta t)-\frac{1}{2}g(\delta t)^2\right)^2=\left(d+\frac{1}{2}a_2(\delta t)^2\right)^2\)
egyenlet fejezi ki. Ebből a \(\displaystyle (\delta t)\)-ben köbös és negyedrendű tagokat elhanyagolva
\(\displaystyle a_2=\frac{v_0^2}{d}=2g\)
adódik, így
\(\displaystyle K_2=6mg.\)
Megjegyzés. Figyelemre méltó, hogy amíg a szélső helyzetben a kötél gyorsulása a gyöngy gyorsulásának a fonal irányába mutató komponense, amikor a gyöngy a kiinduló helyzeten áthalad, a gyorsulása nem, csak a sebessége befolyásolja a fonal gyorsulását. A megoldásban alkalmazott módszerrel nem nehéz belátnunk, hogy egy tetszőleges, \(\displaystyle x_1\), \(\displaystyle x_2\), \(\displaystyle v_1\), \(\displaystyle v_2\), és \(\displaystyle a_1\), \(\displaystyle a_2\) adatokkal jellemzett közbülső helyzetben
\(\displaystyle v_2=v_1\sin\phi,\qquad\textrm{és}\qquad a_2=a_1\sin\phi+\frac{\left(v_1\cos\phi\right)^2}{\sqrt{d^2+x_1^2}},\)
ahol \(\displaystyle \phi\) a fonal gyöngyhöz csatlakozó részének a vízszintessel bezárt szöge (\(\displaystyle \sin\phi=x_1/\sqrt{x_1^2+d^2}\)).
Statistics:
19 students sent a solution. 5 points: Simon János Dániel. 4 points: Erdélyi Dominik, Sütő Áron, Tóth Hanga Katalin. 3 points: 8 students. 2 points: 1 student. 1 point: 3 students.
Problems in Physics of KöMaL, January 2025
