Problem P. 5622. (January 2025)

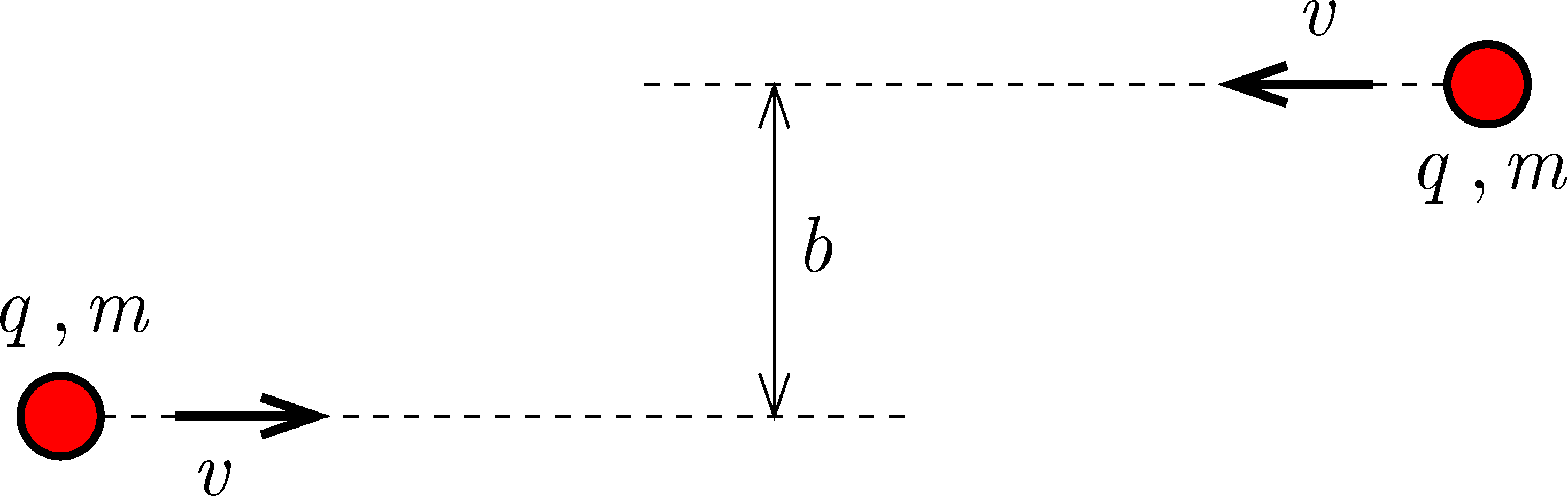
P. 5622. Two small insulating disks of mass \(\displaystyle m\) and of charge \(\displaystyle q\) are placed far apart on a horizontal, frictionless, insulating table top. They move initially in opposite directions, travelling at a speed of \(\displaystyle v\). If they had no charge, they would move along the lines at a distance of \(\displaystyle b\), as shown in the figure. What will the minimum velocity of the two discs be during their motion?

(5 pont)

Deadline expired on February 17, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Mivel a két töltésből álló rendszerben csak belső erők hatnak, a teljes lendület időben állandó, azaz mindvégig zérus. Ezzel ekvivalens tulajdonság, hogy a rendszer tömegközéppontja végig mozdulatlan. A Coulomb-erők centrálisak is, így minden pillanatban a tömegközépponttól elfele mutatnak, és eredő forgatónyomatékot nem fejtenek ki. Ez pedig már implikálja a perdület megmaradását.

Jelölje a keresett minimális sebességet \(\displaystyle u\), a testek távolságát ennek elérésekor pedig \(\displaystyle d\). A szélsőérték-tulajdonság következménye, hogy ebben a pillanatban a testek sebessége merőleges az őket összekötő szakaszra, így a perdületmegmaradás alakja:

\(\displaystyle mvb=mud.\)

Teljesül emellett az energiamegmaradás törvénye is:

\(\displaystyle 2\cdot\frac{1}{2}mv^2=2\cdot\frac{1}{2}mu^2+\frac{kq^2}{d}.\)

Az egyenletekből \(\displaystyle d\) kiküszöbölhető, az eredmény egy másodfokú egyenlet az \(\displaystyle u\) változóra:

\(\displaystyle u^2+\frac{kq^2}{mvb}u-v^2=0.\)

A fizikailag releváns pozitív megoldásból adódik a végeredmény:

\(\displaystyle u=\sqrt{v^2+\left(\frac{kq^2}{2mvb}\right)^2}-\frac{kq^2}{2mvb}.\)

Statistics:

15 students sent a solution.
5 points:	Beke Márton Csaba, Elekes Panni, Erdélyi Dominik, Gyenes Károly, Kovács Tamás, Simon János Dániel, Tóth Hanga Katalin, Tóthpál-Demeter Márk, Ujpál Bálint.
4 points:	Ujvári Sarolta.
3 points:	3 students.
2 points:	1 student.

Problems in Physics of KöMaL, January 2025