 Problem P. 5624. (January 2025)
Problem P. 5624. (January 2025)
P. 5624. Two identical, thin rods are connected at one end by a hinge, around which they are free to turn. Initially the two rods are positioned along a straight line, one rod is stationary, and the free end of the other rod moves at some speed. The rods are free to move in a state of weightlessness, with no external forces acting on them and also friction is negligible. What is the minimum angle between the two rods during their further motions?
(6 pont)
Deadline expired on February 17, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen az egyes rudak tömege \(\displaystyle m\), hossza \(\displaystyle \ell\) és a mozgásban lévő rúd szabad végének sebessége \(\displaystyle v\). A mozgás során a rudak mindvégig a kezdeti sebesség és a rudak kezdeti helyzete által meghatározott síkban maradnak. A két rúdból álló zárt rendszer mozgási energiája is és a perdülete is a mozgás során állandó marad.
Kezdetben az egyik (az 1. ábrán a jobb oldali) rúd tömegközéppontja \(\displaystyle v/2\) sebességgel mozog (felfelé) és \(\displaystyle v/\ell\) szögsebességgel forog, a másik rúd áll. Az egész rendszer impulzusa \(\displaystyle I=mv/2\), a rendszer tömegközéppontjának sebessége tehát \(\displaystyle v_\textrm{tkp}=I/(2m)=v/4\).
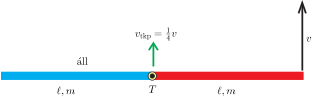
1. ábra
Térjünk át a két rúd tömegközéppontjához rögzített koordináta-rendszerre. Ebben a rendszerben a bal oldali rúd mindkét vége \(\displaystyle v/4\) sebességgel mozog lefelé és a szögsebessége nulla. A jobb oldali rúd egyik vége \(\displaystyle 3v/4\) sebességgel mozog felfelé, a másik vége \(\displaystyle v/4\) sebességgel lefelé, a szögsebessége tehát \(\displaystyle v/\ell\) (lásd a 2. ábrát).
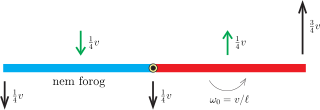
2. ábra
A rendszer mozgási energiája a tömegközépponti rendszerben
| \(\displaystyle (1)\) | \(\displaystyle E=2\cdot\frac{1}{2}m\left(\frac{v}{4}\right)^2+\frac{1}{2}\,\frac{1}{12}m\ell^2\left(\frac{v}{\ell}\right)^2=\frac{5}{48}mv^2.\) |
A rendszer perdülete (ugyancsak a tömegközépponti rendszerben)az egyes rudak saját tömegközéppontjuk körüli forgómozgásából származó ,,sajátperdületének'' és a tömegközéppontjuk mozgásából eredő ,,pályaperdületének" összege:
| \(\displaystyle (2)\) | \(\displaystyle N=0+\frac{1}{4}mv\cdot\frac{\ell}{2}+\frac{1}{12}m\ell^2\cdot\frac{v}{\ell}+\frac{1}{4}mv\cdot\frac{\ell}{2}=\frac{1}{3}mv\ell.\) |
A további mozgás során a rudak általában különböző szögsebességgel mozognak, és emiatt a közrezárt szögük időben változik. Abban a pillanatban, amikor a rudak által bezárt \(\displaystyle 2\varphi\) szög eléri a legkisebb értékét (feltételezve, hogy ilyen minimum valóban létrejön), a rudak relatív szögsebességének pillanatnyi értéke nulla kell, hogy legyen, vagyis mindkét rúd ugyanakkora \(\displaystyle \omega\) szögsebességgel fog forogni a rendszer tömegközéppontja körül (3. ábra). Azt is mondhatjuk, hogy a két rúd ebben a pillanatban merev testként viselkedik.
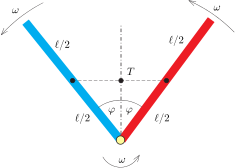
3. ábra
Legyen a két rúdból álló rendszer tehetetlenségi nyomatéka a legkisebb közrezárt szögnél a rendszer \(\displaystyle T\) tömegközéppontjára vonatkoztatva \(\displaystyle \varTheta\). Ekkor az összenergia
\(\displaystyle E=\frac{1}{2}\varTheta\omega^2,\)
az összperdület pedig
\(\displaystyle N=\varTheta\,\omega\)
módon számítható. Látszik, hogy az \(\displaystyle N^2/(2E)\) mennyiségből kiesik a szögsebesség:
| \(\displaystyle (3)\) | \(\displaystyle \frac{N^2}{2E}=\varTheta.\) |
(3) bal oldala (1) és (2)-ből adódóan
\(\displaystyle \frac{N^2}{2E}=\frac{8}{15}m\ell^2,\)
a jobb oldala pedig a Steiner-tétel felhasználásával
\(\displaystyle \varTheta=2\cdot\left[\frac{1}{12}m\ell^2+m\left(\frac{\ell}{2}\sin\varphi\right)^2\right]=\left(\frac{1}{6}+\frac {\sin^2\varphi}2\right)m\ell^2.\)
A fenti két kifejezés egyenlőségéből
\(\displaystyle \frac{8}{15}=\frac{1}{6}+\frac{\sin^2\varphi}2,\)
vagyis
\(\displaystyle \sin\varphi=\sqrt{\frac{11}{15}}\)
következik, vagyis a rudak által bezárt legkisebb szög
\(\displaystyle 2\varphi=2\arcsin\sqrt{\frac{11}{15}}\approx 118^\circ.\)
Statistics:
11 students sent a solution. 6 points: Beke Márton Csaba, Erdélyi Dominik, Fajszi Karsa, Kovács Tamás, Tóth Hanga Katalin. 5 points: Ujpál Bálint, Zólomy Csanád Zsolt. 4 points: 2 students. 3 points: 1 student. 2 points: 1 student.
Problems in Physics of KöMaL, January 2025
