 Problem P. 5631. (February 2025)
Problem P. 5631. (February 2025)
P. 5631. The electric field strength at a distance \(\displaystyle R\) from a uniformly charged, thin, very long, straight filament is well known. Compare this field strength with the electric field strength at the centre of a bent filament, having a shape of a semicircle of radius \(\displaystyle R\). The filaments have the same properties and the same linear charge density.
(5 pont)
Deadline expired on March 17, 2025.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Legyen a szál vonalmenti töltéssűrűsége (egységnyi hosszúságú darabjának töltése) \(\displaystyle \lambda\). A nagyon hosszú, egyenes száltól \(\displaystyle R\) távolságban az elektromos térerősség nagysága
| \(\displaystyle (1)\) | \(\displaystyle E_1=\frac{1}{2\pi\varepsilon_0}\,\frac{\lambda}{R},\) |
amit a \(\displaystyle k=1/(4\pi\varepsilon_0)\) Coulomb-állandóval kifejezve így is felírhatunk:
| \(\displaystyle (1')\) | \(\displaystyle E_1=2k\frac{\lambda}{R}.\) |
Megjegyzés. A fenti képlet helyességét pl. a Gauss-féle fluxustörvényből is megkaphatjuk. A szál \(\displaystyle \ell\) hosszúságú darabjának töltése \(\displaystyle Q=\lambda\ell\). Ha a szálat koaxiálisan körülvesszük egy \(\displaystyle R\) sugarú hengerrel, annak palástjára vonatkoztatott elektromos fluxus \(\displaystyle \Psi=2R\pi\ell E_1.\) A fluxustörvény szerint \(\displaystyle \Psi=\tfrac{1}{\varepsilon_0}Q\), ezekből pedig (1) már következik.
Tekintsük most az \(\displaystyle R\) sugarú, félkör alakú szál esetét. A félkör \(\displaystyle O\) középpontjában az elektromos térerősség iránya a félkör szimmetriatengelye, nagysága pedig legyen \(\displaystyle E_2\). Ha a félkör középpontjába egy \(\displaystyle q\) nagyságú ponttöltést helyezünk, arra \(\displaystyle qE_2\) nagyságú erő hat. Ugyanekkora nagyságú, de ellentétes irányú erőt fejt ki a ponttöltés az egyenletesen töltött szálra.
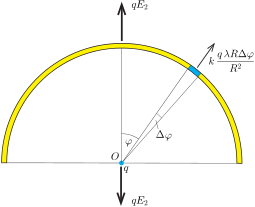
1. ábra
A félkör alakú szálnak egy kicsiny, \(\displaystyle O\)-ból nézve \(\displaystyle \Delta\varphi\) szög alatt látszó darabkájának töltése \(\displaystyle \lambda R\Delta\varphi,\) erre tehát a \(\displaystyle q\) töltés
\(\displaystyle \Delta F=k\frac{q\,\lambda R\Delta\varphi}{R^2}\)
nagyságú, sugár irányban ,,kifelé'' mutató erőt fejt ki. Ezen erőnek a szimmetriatengely irányú komponense \(\displaystyle \Delta F \cos\varphi\), ahonnan az egyes darabkák járulékainak összegzésével kapjuk, hogy
\(\displaystyle qE_2=\sum k\frac{q\,\lambda R\Delta\varphi}{R^2}\,\cos\varphi.\)
Innen – a felosztás finomításával integrálásra áttérve – adódik a keresett eredmény:
\(\displaystyle E_2=k\frac{\lambda}{R}\int\limits_{-\pi/2}^{\pi/2}\cos\varphi\,\mathrm{d}\varphi.\)
Az integrál számértéke 2, így (1')-vel összevetve megállapíthatjuk, hogy \(\displaystyle E_2=E_1\), vagyis a kétféle elrendezés térerőssége a vizsgált pontban ugyanakkora.
Megjegyzés. A félkörre ható eredő erő nagyságát integrálszámítás nélkül is meghatározhatjuk. Megállapíthatjuk, hogy a félkör alakú szálra hosszegységenként \(\displaystyle p=kq\lambda/R^2\) nagyságú, a száldarabka érintőjére merőleges irányú erő hat. (\(\displaystyle p\) a folyadékok nyomásához hasonló, ,,vonalmenti nyomásként'' értelmezhető mennyiség.) Egészítsük ki a félkör-szálat egy a végpontjai között elhelyezkedő, \(\displaystyle 2R\) hosszúságú egyenes darabbal, aminek ugyanakkora a töltéssűrűsége, mint a félköré. Ha erre az egyenes szálra is \(\displaystyle p\) ,,nyomást'', tehát \(\displaystyle 2Rp\) nagyságú erőt fejtünk ki, akkor a zárt hurokra ható eredő erő nullává válik. (Analóg helyzet: egy zárt tartályra a benne lévő gáz nyomása nem fejt ki eredő erőt.) Ennek megfelelően a félkörre ható \(\displaystyle qE_2\) elektromos erő is \(\displaystyle 2Rp=2kq\lambda/R\) nagyságú, azaz \(\displaystyle E_2=E_1\) teljesül.
II. megoldás. A két töltött szál \(\displaystyle O\) pontbeli elektromos térerősségét anélkül is össze tudjuk hasonlítani, hogy bármelyik térerősség nagyságát kiszámítanánk. Megmutatjuk, hogy a két szál egymásnak megfeleltethető kicsiny darabkáinak térerőssége ugyanolyan irányú és ugyanolyan nagyságú vektor, emiatt ezeknek a vektoroknak az összege, vagyis az eredő elektromos térerősség a kétféle alakú szálra ugyanakkora.
Tekintsük a félkörív és az egyenes szál azon kicsiny darabkáit, amelyek az \(\displaystyle O\) pontból nézve ugyanolyan irányban és ugyanakkora szög alatt látszanak.
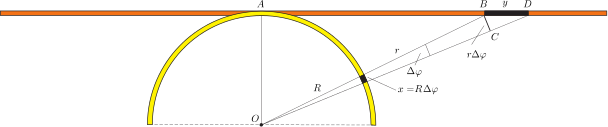
2. ábra
A 2. ábra jelöléseit követve megállapíthatjuk, hogy a körív alakú szál kicsiny \(\displaystyle x=R\Delta\varphi\) hosszúságú ívén \(\displaystyle Q_1=\lambda x\) töltés, az egyenes szál \(\displaystyle y\) hosszúságú részén pedig \(\displaystyle Q_2=\lambda y\) töltés található. Ezek a töltések az \(\displaystyle O\) pontban
\(\displaystyle E_1=k\lambda\frac{x}{R^2},\qquad\textrm{illetve}\qquad E_2=k\lambda\frac{y}{r^2}\)
nagyságú elektromos térerősséget hoznak létre. Ez a két térerősség azonban egyforma nagy, hiszen az \(\displaystyle OAB\triangle\) és a \(\displaystyle BCD\triangle\) hasonlósága miatt
\(\displaystyle \frac{r}{R}=\frac{y}{r\Delta\varphi}=\frac{yR}{xr},\qquad\textrm{tehát}\qquad\frac{y}{r^2}=\frac{x}{R^2}.\)
A fenti megfontolások során kihasználtuk, hogy \(\displaystyle x\ll R\) és \(\displaystyle y\ll r\), vagyis a szálak kis darabkáinak látószöge nagyon kicsi, emiatt a kicsiny körívek hossza és a megfelelő húrok hossza egyenlőnek vehető.
Statistics:
22 students sent a solution. 5 points: Beke Márton Csaba, Bélteki Teó, Erdélyi Dominik, Gyenes Károly, Kiss 131 Adorján Timon, Klement Tamás, Simon János Dániel, Szécsi Bence, Tóth Hanga Katalin, Ujpál Bálint, Zólomy Csanád Zsolt. 4 points: Hornok Máté, Kovács Tamás, Papp Emese Petra, Ujvári Sarolta. 3 points: 1 student. 1 point: 2 students.
Problems in Physics of KöMaL, February 2025
