 Problem P. 5632. (February 2025)
Problem P. 5632. (February 2025)
P. 5632. On one side of a large metal plate, there is a point-like ball of charge \(\displaystyle Q\) and another of charge \(\displaystyle -Q\), at a distance of \(\displaystyle d\) from each other and \(\displaystyle d/2\) from the plate. How much work is needed
a) to move the charges parallel to the plane of the plate, and separate them very far from each other,
b) to move the charges perpendicular to the plate and carry them very far away from the plate (to the same distance),
c) to move the charges very far away from the plate and from each other?
(5 pont)
Deadline expired on March 17, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Egy nagy méretű fémlemez egyik oldalán lévő kicsiny töltés megosztást hoz létre a fémlemezben, és a kialakuló elektromos mező olyan lesz, mintha a kis töltés helyének a lemezre vett tükörkép-pontjában egy vele azonos nagyságú, de ellentétes töltésű másik test, az úgynevezett tükörtöltés helyezkedne el. Ez az elektromos mező a fémlemeznek csak az egyik (a valódi töltéssel megegyező) oldalán alakul ki, a másik oldalon a térerősség mindenhol nulla.
Két kicsiny töltött test és a nagy méretű fémlemez elektromos terét a két töltés és a nekik megfelelő két tükörtöltés együttese határozza meg (lásd az ábrát).
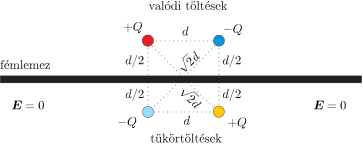
Egy ilyen elrendezés elektrosztatikus (kölcsönhatási) energiáját a páronkénti Coulomb-energiák összege adja meg, de mivel elektromos mező a fémlemeznek csak az egyik oldalán alakul ki, az összenergia csak a fele annak, amekkora 4 valódi töltés esetében lenne. Esetünkben a kezdeti elrendezés energiája
\(\displaystyle {\cal E}_0=\frac{1}{2}\cdot kQ^2\left(-\frac{1}{d}-\frac{1}{d}-\frac{1}{d}-\frac{1}{d}+\frac{1}{\sqrt{2}d}+ \frac{1}{\sqrt{2}d}\right)=\frac{kQ^2}{d}\left(\frac{1}{\sqrt{2}}-2\right).\)
Hasonló módon számíthatjuk ki a különböző módon eltávolított töltések elektrosztatikus energiáját is:
\(\displaystyle {\cal E}_a={\cal E}_b=-\frac{kQ^2}{d}\qquad\textrm{és}\qquad{\cal E}_c=0.\)
(Az egymástól ,,nagyon messzire'' kerülő töltések kölcsönhatási energiája – jó közelítéssel – nullának tekinthető.)
A töltések megadott módon történő elmozdítása során végzett munka az elektrosztatikus energia megváltozásával (növekedésével) egyenlő.
\(\displaystyle W_a={\cal E}_a-{\cal E}_0=\frac{kQ^2}{d}\left(1-\frac{1}{\sqrt{2}}\right),\)
\(\displaystyle W_b={\cal E}_b-{\cal E}_0=\frac{kQ^2}{d}\left(1-\frac{1}{\sqrt{2}}\right),\)
\(\displaystyle W_c={\cal E}_c-{\cal E}_0=\frac{kQ^2}{d}\left(2-\frac{1}{\sqrt{2}}\right).\)
Statistics:
6 students sent a solution. 4 points: Kovács Tamás, Simon János Dániel, Ujpál Bálint, Vértesi Janka. 3 points: 1 student. 2 points: 1 student.
Problems in Physics of KöMaL, February 2025
