 Problem P. 5638. (March 2025)
Problem P. 5638. (March 2025)
P. 5638. A point charge \(\displaystyle Q\) on the outside of a neutral metal sphere, at a distance of \(\displaystyle d\) from the centre of the sphere, is moved to a distance of \(\displaystyle 2d\). How much does the potential of the metal sphere change during this process?
(5 pont)
Deadline expired on April 15, 2025.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Egy fémgömb közelébe helyezett ponttöltés megosztást hoz létre a fémgömbön. A töltések úgy mozdulnak el a fém felületén, hogy a gömb ekvipotenciálissá váljon. A kialakuló elektromos mező a gömbön kívül olyan, mintha a gömb belsejében megfelelő helyen megfelelő nagyságú ,,tükörtöltés'' helyezkedne el, és a fém nem is lenne ott. (Ez a gömbi tükörtöltés módszere, amelyről részletesen olvashatunk pl. a KöMaL 2022. évi decemberi számában megjelent P. 5453. feladat megoldásánál.)
Ha egy \(\displaystyle R\) sugarú fémgömb középpontjától \(\displaystyle d\) távolságra egy pontszerű \(\displaystyle Q\) töltés található, akkor a fémfelület akkor válik nulla potenciálúvá, ha a gömb középpontjától \(\displaystyle x=R^2/d\) távolságban egy \(\displaystyle q=-\frac{R}{d}Q\) nagyságú tükörtöltést helyezünk el. Ha a fémgömb nem földelt, de az össztöltése nulla, akkor a gömbhéj potenciálja nem lesz nulla, de a felülete továbbra is ekvipotenciális marad. Ezt az erőteret a külső \(\displaystyle Q\) töltés, a gömbön belüli \(\displaystyle q\) töltés, valamint a gömb középpontjába helyezett \(\displaystyle -q=\frac{R}{d}Q\) töltés tudja létrehozni. A fémgömb potenciálja ilyenkor
\(\displaystyle \Phi(d)=-\frac{1}{4\pi\varepsilon_0}\frac{q}{R}=\frac{1}{4\pi\varepsilon_0}\frac{Q}{d}\)
lesz. (A potenciált a ,,végtelen'' távoli pontokban választottuk nullának.)
Ha a \(\displaystyle Q\) töltést \(\displaystyle 2d\) távolra visszük, a fémgömb potenciálja
\(\displaystyle \Phi(2d)=\frac{1}{4\pi\varepsilon_0}\frac{Q}{2d}\)
lesz. A potenciál megváltozása
\(\displaystyle \Delta\Phi=\Phi(2d)-\Phi(d)=-\frac{1}{4\pi\varepsilon_0}\frac{Q}{2d}.\)
Ha \(\displaystyle Q>0,\) akkor \(\displaystyle \Delta\Phi<0,\) vagyis a fémgömb elektromos potenciálja lecsökken.
II. megoldás. A feladatot a gömbi tükörtöltés módszerének ismerete nélkül is meg lehet oldani. Tekintsük a fémgömb és a pontszerű töltés rendszerének az ábrán látható 4-féle állapotát:
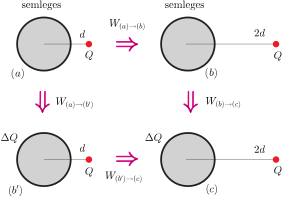
(a) Kezdetben a fémgömb semleges, és a \(\displaystyle Q\) töltés a gömb középpontjától \(\displaystyle d\) távolságra van.
(b) A fémgömb semleges, de a ponttöltést a gömb középpontjától \(\displaystyle 2d\) távolságra található.
(b') A ponttöltés \(\displaystyle d\) távolságra van a gömb középpontjától, de a fémgömb nem semleges, hanem kicsiny, \(\displaystyle \Delta Q\ll Q\) töltéssel rendelkezik.
(c) A ponttöltés \(\displaystyle 2d\) távolságra van a \(\displaystyle \Delta Q\) töltésű gömb középpontjától.
Számítsuk ki, hogy mekkora munkavégzéssel tudjuk a rendszert az (a) állapotból egyszer (b)-n, másodszor pedig (b')-n keresztül a (c) állapotba vinni.
A \(\displaystyle Q\) töltés a semleges fémgömbön elektromos megosztást hoz létre, amelynek elektromos mezője valamilyen (helyről helyre változó) erőt fejt ki a ponttöltésre. A \(\displaystyle Q\) töltést valamekkora
\(\displaystyle W_{(a)\rightarrow(b)}=W_0\)
munkát végezve juttathatjuk el \(\displaystyle d\)-től \(\displaystyle 2d\) távolságig. (Ennek a munkának a nagyságát ki lehet számítani, de erre – szerencsére – nem lesz szükségünk.)
Ha a (b) állapotban a fémgömb potenciálja \(\displaystyle \Phi(2d)\), akkor nagyon (,,végtelen'') messziről kicsiny \(\displaystyle \Delta Q\) töltést
\(\displaystyle W_{(b)\rightarrow(c)}=\Delta Q\cdot\Phi(2d)\)
munkával tudunk a fémgömbre juttatni. (Ez a potenciál definíciójából következik.)
Járjuk most végig a másik ,,útvonalat''. A fémgömbre
\(\displaystyle W_{(a)\rightarrow(b')}=\Delta Q\cdot\Phi(d)\)
munkával tudunk \(\displaystyle \Delta Q\) töltést eljuttatni, ahol \(\displaystyle \Phi(d)\) a fémgömb potenciálja a \(\displaystyle Q\) töltés közelebbi helyzetében.
Végül számítsuk ki, hogy mekkora munkával tudjuk a kicsiny töltéssel rendelkező gömbtől a \(\displaystyle Q\) töltést \(\displaystyle d\)-től \(\displaystyle 2d\)-ig eltávolítani. Az elektromos erőtér ebben az esetben a megosztásból származó térerősségek és a \(\displaystyle \Delta Q\) töltés elektromos terének szuperpozíciója. Az előbbi erőtérben végzett munka a korábban szereplő \(\displaystyle W_0\)-lal egyezik meg. A \(\displaystyle \Delta Q\) töltés által létrehozott elektromos mező – a gömbön kívül – egy pontszerű töltés Coulomb-terével egyezik meg, ennek ellenében végzett munka tehát a Coulomb-energia megváltozásával egyenlő. Így
\(\displaystyle W_{(b')\rightarrow(c)}=W_0+\frac{Q\cdot\Delta Q}{4\pi\varepsilon_0}\left(\frac{1}{2d}-\frac{1}{d}\right).\)
A végzett munka az elektromos mező energiájának megváltozásával egyenlő, emiatt független attól, hogy milyen közbenső állapoton keresztül jutottunk el (a)-ból (c)-be:
\(\displaystyle W_{(a)\rightarrow(b)}+W_{(b)\rightarrow(c)}=W_{(a)\rightarrow(b')}+W_{(b')\rightarrow(c)},\)
azaz
\(\displaystyle W_0+\Delta Q\cdot\Phi(2d)=\Delta Q\cdot\Phi(d)+\left(W_0-\frac{Q\cdot\Delta Q}{4\pi\varepsilon_0}\frac{1}{2d}\right).\)
Innen kapjuk, hogy a fémgömb potenciáljának megváltozása
\(\displaystyle \Phi(2d)-\Phi(d)=-\frac{1}{4\pi\varepsilon_0}\frac{Q}{2d}.\)
III. megoldás. A \(\displaystyle \Phi(d)\) potenciált egy egyszerű meggondolással is megkaphatjuk. A fémgömb felületén a \(\displaystyle Q\) töltés okozta elektromos megosztás miatt valamilyen \(\displaystyle \varrho(\vec{R})\) töltéssűrűség alakul ki, és a tér bármely pontjában a potenciál ezen töltéseloszlás és a különálló \(\displaystyle Q\) töltés potenciáljának összegeként adható meg. Mivel a fémgömb minden pontja azonos potenciálon van, ennek meghatározásához kézenfekvő, hogy a legegyszerűbb leírást kínáló pontot, a gömb középpontját válasszuk. A gömbfelület \(\displaystyle \vec{R}\)-rel jellemezhető pontja körüli kis \(\displaystyle \Delta A\) felület töltése \(\displaystyle \Delta q=\varrho(\vec{R})\Delta A\), így
\(\displaystyle \Phi(d)=\frac{1}{4\pi\varepsilon_0}\sum\frac{\Delta q}{R}+\frac{1}{4\pi\varepsilon_0}\frac{Q}{d}.\)
Mivel a gömb semleges, \(\displaystyle \sum\Delta q=0\), tehát
\(\displaystyle \Phi(d)=\frac{1}{4\pi\varepsilon_0}\frac{Q}{d}.\)
Statistics:
19 students sent a solution. 5 points: Beke Márton Csaba, Erdélyi Dominik, Klement Tamás, Pituk Péter, Poló Zsófia , Simon János Dániel, Tóth Bertalan, Varga Zétény. 4 points: Balázs Barnabás, Bor Noémi, Kávai Ádám, Konkoly Zoltán, Ujvári Sarolta. 3 points: 2 students. 2 points: 2 students.
Problems in Physics of KöMaL, March 2025
