 Problem P. 5639. (March 2025)
Problem P. 5639. (March 2025)
P. 5639. In the circuit assembled according to the attached circuit diagram, the voltage supply has an electromotive force of 6 V and an internal resistance of \(\displaystyle 2\,\Omega\). The inductance of the ideal coil is \(\displaystyle 1.5~\mathrm{H}\) and the resistance of resistor \(\displaystyle R\) is \(\displaystyle 1000\,\Omega\). Initially, the switch is closed.
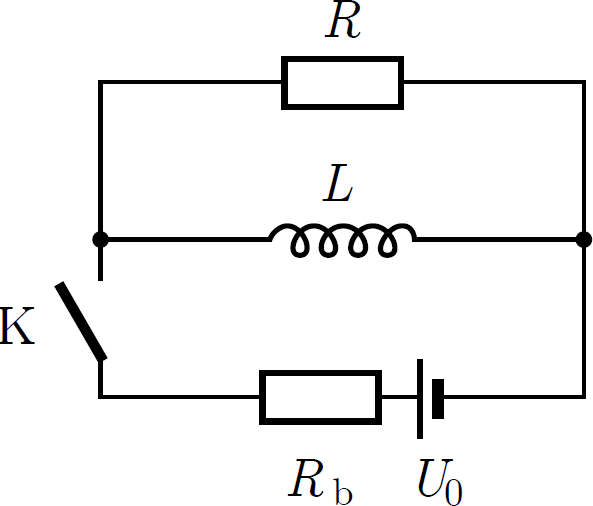
a) How much charge flows through resistor \(\displaystyle R\) after the switch is opened?
b) How much heat is dissipated in resistor \(\displaystyle R\) during this time?
(5 pont)
Deadline expired on April 15, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Amíg a kapcsoló zárva van az \(\displaystyle R\) ellenálláson nem folyik áram (olyan, mintha ott se lenne), hiszen az ,,ideális'' tekercs ellenállása (időben állandó áram esetében) elhanyagolható. A tekercsen átfolyó áram (1. ábra):
\(\displaystyle I_0=\frac{U_0}{R_\mathrm{b}}=3\,\mathrm{A}.\)

1. ábra
A kapcsoló kinyitása (\(\displaystyle t=0\)) után a tekercs árama nem változhat ugrásszerűen, így az \(\displaystyle R\) ellenálláson \(\displaystyle I(0)=I_0=3\,\mathrm{A}\) áram kezd folyni, és \(\displaystyle U(0)=RI(0)=RI_0=3000\,\mathrm{V}\) feszültség fog esni. Ugyanekkora nagyságú – de a rajta átfolyó áram irányához viszonyítva ellentétes irányú – a tekercs feszültsége is (2. ábra).
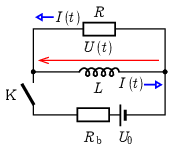
2. ábra
Ebből meghatározhatjuk az áram változási sebességét:
$$\begin{gather*} L\frac{\mathrm{d}I(t)}{\mathrm{d}t}=-U(t)=-RI(t),\\ \frac{\mathrm{d}I(t)}{\mathrm{d}t}=-\frac{R}{L}I(t). \end{gather*}$$Ez egy időben exponenciálisan lecsengő áramot ír le, de a függvény meghatározására nincsen szükségünk. Az egyenletet szorozzuk át \(\displaystyle -\tfrac{L}{R}\)-rel és formálisan \(\displaystyle \mathrm{d}t\)-vel, így megkapjuk, mekkora töltés áramlik át egy kicsiny \(\displaystyle \mathrm{d}t\) idő alatt:
\(\displaystyle \mathrm{d}q=I(t)\mathrm{d}t=-\frac{L}{R}\mathrm{d}I.\)
Ebből egyszerű összegzéssel megkapjuk a lecsengési folyamat során átáramló össztöltést:
\(\displaystyle q=\sum\mathrm{d}q=\sum_0^\infty I(t)\mathrm{d}t=-\frac{L}{R}\sum_0^\infty\mathrm{d}I=-\frac{L}{R}(-I_0)=\frac{L}{R}I_0=\frac{L}{R}\frac{U_0}{R_\mathrm{b}}=4{,}5\,\mathrm{mC}.\)
Megjegyzés. Az áram időfüggésére felírt differenciálegyenletnek jól ismerjük a megoldását (ilyen a radioaktív bomlást leíró összefüggés is):
\(\displaystyle I(t)=I_0\mathrm{e}^{-\frac{t}{\tau}},\)
ahol
\(\displaystyle \tau=\frac{L}{R}=1{,}5\,\mathrm{ms}.\)
Ezután az átáramló össztöltést meghatározhatjuk az áram integrálásával a lecsengés teljes ideje alatt:
\(\displaystyle q=\int\limits_0^\infty I(t)\mathrm{d}t=\int\limits_0^\infty I_0\mathrm{e}^{-\frac{t}{\tau}}\mathrm{d}t=\left[-\tau I_0\mathrm{e}^{-\frac{t}{\tau}}\right]_0^\infty=\tau I_0=\frac{L}{R}\frac{U_0}{R_\mathrm{b}},\)
az előbb kapott eredménnyel összhangban.
A ,,végtelen'' ideig tartó összegzés furcsának tűnik, de valójában a lecsengés az időállandó tízszerese (tehát 15 ezredmásodperc) alatt lényegében lejátszódik.
b) Az ellenálláson annyi hő fejlődik, amekkora a kapcsoló nyitásának pillanatában a tekercs mágneses energiája volt:
\(\displaystyle Q=E_\textrm{m}=\frac{1}{2}LI_0^2=6{,}75\,\mathrm{J}.\)
Megjegyzés. A hőt megkaphatjuk a változó áram Joule-teljesítményének összegzésével is:
\(\displaystyle Q=\int\limits_0^\infty P(t)\mathrm{d}t=\int\limits_0^\infty R\left[I(t)\right]^2\mathrm{d}t=RI_0^2\int\limits_0^\infty \mathrm{e}^{-2\frac{t}{\tau}}\mathrm{d}t=-\frac{\tau}{2}RI_0^2\left[\mathrm{e}^{-2\frac{t}{\tau}}\right]_0^\infty=\frac{\tau}{2}RI_0^2=\frac{1}{2}LI_0^2,\)
az előző megoldással összhangban.
Statistics:
22 students sent a solution. 5 points: Beke Márton Csaba, Bélteki Teó, Benyó Júlia , Erdélyi Dominik, Kiss 131 Adorján Timon, Klement Tamás, Masa Barnabás, Simon János Dániel, Tóth Hanga Katalin, Ujpál Bálint, Ujvári Sarolta. 4 points: Fekete Lúcia, Sütő Áron, Tóthpál-Demeter Márk. 3 points: 2 students. 2 points: 2 students. 0 point: 1 student.
Problems in Physics of KöMaL, March 2025
